Электронное пособие по теме “Функциональные последовательности и ряды"
Формирование ответа.
Нахождение суммы функционального ряда
Определение области сходимости функционального ряда.
Нахождение суммы функционального ряда с учетом его области сходимости (использование формул суммы геометрической прогрессии).
После подведения итогов оговаривается домашнее задание.
Домашнее задание: практическое занятие №12 из.
Ниже приведены решенные номера домашнего задания:
Пример №10 (№47из ).
Исследовать сходимость функционального ряда
![]()
в точках ![]() и
и ![]() .
.
Решение
Если ![]() , то ряд примет вид:
, то ряд примет вид: ![]() - числовой положительный ряд.
- числовой положительный ряд.
Исследуем полученный числовой ряд на сходимость, применив признак Даламбера сходимости числового ряда:
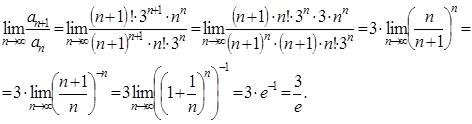
Так как ![]() , то полученный числовой ряд расходится. Значит, функциональный ряд в точке
, то полученный числовой ряд расходится. Значит, функциональный ряд в точке ![]() расходится.
расходится.
Если ![]() , то получится числовой положительный ряд вида:
, то получится числовой положительный ряд вида: ![]() . Исследуем полученный числовой ряд на сходимость, применив признак Даламбера сходимости числового ряда:
. Исследуем полученный числовой ряд на сходимость, применив признак Даламбера сходимости числового ряда:
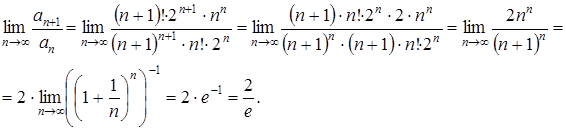
Так как ![]() , то полученный числовой ряд сходится абсолютно. Значит, исследуемый функциональный ряд в точке
, то полученный числовой ряд сходится абсолютно. Значит, исследуемый функциональный ряд в точке ![]() сходится абсолютно.
сходится абсолютно.
Ответ: заданный функциональный ряд сходится абсолютно в точке ![]() и расходится при
и расходится при ![]()
Пример №11 (№30 из).
Найти область сходимости ряда
![]() .
.
Решение
По признаку Даламбера абсолютной сходимости функционального ря-да можно записать:
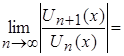
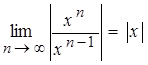 ,
,
Если ![]() , т.е.
, т.е. ![]() , то заданный функциональный ряд
, то заданный функциональный ряд 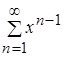 сходится абсолютно на интервале
сходится абсолютно на интервале ![]() .
.
Если ![]() , т.е.
, т.е. ![]() , то ряд
, то ряд ![]() расходится в соответствии с признаком Даламбера абсолютной сходимости функционального ряда.
расходится в соответствии с признаком Даламбера абсолютной сходимости функционального ряда.
При![]() функциональный ряд становится числовым знакочередующимся рядом вида 1-1+1-…. Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а)
функциональный ряд становится числовым знакочередующимся рядом вида 1-1+1-…. Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а) ![]() ; б)
; б) ![]() . Значит, функциональный ряд
. Значит, функциональный ряд 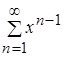 в точке
в точке ![]() расходится.
расходится.
При ![]() функциональный ряд становится числовым положительным рядом вида 1+1+1+…. Он расходится, так как не выполняется необходимое условие сходимости числового ряда, т.е.
функциональный ряд становится числовым положительным рядом вида 1+1+1+…. Он расходится, так как не выполняется необходимое условие сходимости числового ряда, т.е. ![]() . Значит, функциональный ряд
. Значит, функциональный ряд ![]() в точке
в точке ![]() расходится.
расходится.
Образование, педагогика, воспитание:
Уровни образования. Особенности организации и финансирования образования
Образовательная система Республики Кореи включает: дошкольные учреждения и детские сады, срок обучения в которых составляет от одного до трех лет; шестилетние начальные школы; трехлетние средние школы; трехлетние средние школы повышенной ступени; колледжи и университеты со сроком обучения в четыре ...
Мультимедиа - средство обучения нового поколения
Современное образование требует изменения подходов к обучению. Прежде всего, следует добиться максимальной активизации и визуализации обучения. Этому способствует применение различных технических средств, позволяющих сократить время изложения нужной информации и современные технологии в образовании ...
Повышение квалификации
Вид профессионального обучения работников, имеющий целью повышение уровня их теоретических знаний, совершенствование практических навыков и умений. Повышение квалификации рабочих — это обучение, направленное на последовательное совершенствование их профессиональных и экономических знаний, умений и ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

