Электронное пособие по теме “Функциональные последовательности и ряды"

Ответ: - область сходимости заданного функционального ряда.

Пример №6 (№18 из , студент самостоятельно у доски).

Найти область сходимости функционального ряда:

Решение

По признаку Даламбера абсолютной сходимости функционального ряда можно записать:

.

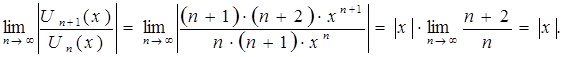Если , т.е. , то заданный функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то ряд расходится.

Исследуем заданный функциональный ряд на сходимость в точках х=1 и х= - 1.

При получается числовой положительный ряд 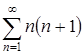. Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда, т.е. . Значит, заданный функциональный ряд в точке расходится.

При получается числовой знакочередующийся ряд вида 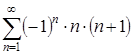. Он является расходящимся, так как не удовлетворяет условиям признака Лейбница: а) ; б) .

Ряд составленный из абсолютных величин элементов ряда имеет вид и является расходящимся.

Значит, исходный функциональный ряд расходится и в точке .

Поэтому, область сходимости заданного функционального ряда интервал - .

Ответ: .

Пример №7 (№28 из [8], студент самостоятельно у доски).

Найти область сходимости функционального ряда:

.

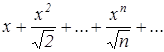Решение. Определим и заданного ряда:

, .

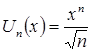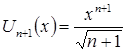По признаку Даламбера абсолютной сходимости функционального ряда имеем:

=

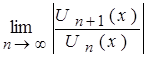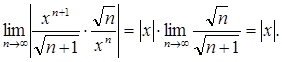
Если , т.е. , то в соответствии с признаком Даламбера абсолютной сходимости функционального ряда, исследуемый функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то функциональный ряд расходится.

Исследуем заданный ряд в точках и .

Образование, педагогика, воспитание:

Работа с кадрами дошкольного учреждения
Современная практика работы дошкольных учреждений показывает, что далеко не все педагоги и родители знают особенности психофизического, эмоционального и интеллектуального развития ребенка-дошкольника и, как следствие, слабо владеют приемами здоровьесберегающей педагогики. Для более эффективного вза ...

Задачи и содержание обучения связной речи
Программа детского сада, предусматривает обучение диалогической и монологической речи. Работа по развитию диалогической речи направлена на формирование умений, необходимых для общения. Диалог – сложная форма социального взаимодействия. Участвовать в диалоге иногда бывает труднее, чем строить моноло ...

Глобализация высшего образования в Европе: предболонский период
Первый период – 1957 – 1982 годы. Конференция министров образования в 1971 году обозначила пять основных моментов общеевропейского измерения в образовательных системах: взаимное признание дипломов; обоснование идеи формирования европейского университета; кооперация вторичного и высшего образования; ...