Электронное пособие по теме “Функциональные последовательности и ряды"

Вопрос 1: Сформулировать определение функциональной последовательности.

Ответ: Определение №1. Пусть дана последовательность функций . Причем функции являются функциями одной переменной и определены в некоторой области . Такая последовательность называется функциональной и обозначается .

Вопрос 2: Определить, что называют предельной функцией последовательности ?

Ответ: Определение №2. Функция называется предельной функцией последовательности , если выполняется утверждение .

Вопрос 3: Дать понятия функционального ряда и его области сходимости.

Ответ: Определение №3. Ряд, элементами которого являются функции одной и той же переменной , заданной в области:

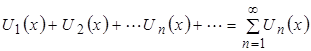
называется функциональным рядом.

Определение №4. Совокупность всех значений переменной , при которых функции определены и ряд 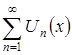сходится, называют областью сходимости функционального ряда.

Областью сходимости функционального ряда чаще всего служит какой-нибудь промежуток оси .

Вопрос 4: Что называют суммой функционального ряда?

Ответ: Пусть дан функциональный ряд 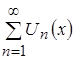и он сходится при каждом фиксированном из, тогда сумму такого ряда представляет собой некоторую функцию переменной : 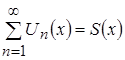. Сумма для функционального ряда определяется также как и для числового: . Здесь - частичная сумма функционального ряда n-го порядка

.

Преподаватель: Итак, а теперь приступим непосредственно к выполнению упражнений.

При объяснении нового материала, на экран телевизора выводится задание с подробным решением, преподаватель комментирует решение, студенты записывают в тетради. При объяснении материала следует обратиться к технологической карте по теме "Функциональные последовательности и ряды", в которой отмечены затруднения при изучении данной темы, а также типичные ошибки, допускаемые студентами.

Практические задания должны рассматриваться по принципу "от простого к сложному". Вначале необходимо выполнить упражнения на исследование сходимости функционального ряда в точке. Такого вида упражнения помогают студентам обнаружить взаимосвязь числового и функционального рядов, а также лучше понять "природу" функционального ряда.

Дан функциональный ряд:

,

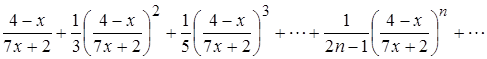Образование, педагогика, воспитание:

Сущность понятия "одаренность"
В современной социально-педагогической литературе существует огромное количество определений понятия одаренность. В толковом словаре русского языка Д.Н. Ушакова одаренность - талантливость, даровитость, та или иная степень ее. Одаренный - человек с богатой природой, обладающий какими-нибудь свойств ...

Отбор грамматического материала для обучения устной речи и чтению
Сущность отбора грамматического материала для школы заключается в создании такого грамматического минимума, который был бы посилен для усвоения и достаточен для выполнения коммуникативно-значимых задач обучения. При решении вопроса об отборе грамматического минимума учитываются источники и принципы ...

Классификация технических средств обучения
Комплекс технических средств, предлагаемых для использования в процессе обучения, год от года становится всё сложнее и многообразнее. От умения педагога эффективно использовать эти средства в немалой степени зависит конечный результат восприятия учениками новой для них информации. Технические средс ...