Электронное пособие по теме “Функциональные последовательности и ряды"

Найдем общий элемент заданного функционального ряда:

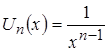
Исследуемый функциональный ряд представляет собой сумму убывающей геометрической прогрессии при , т.е. при , где , .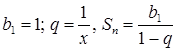

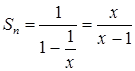Значит, область сходимости исходного функционального ряда: .

Проверим сходимость исходного функционального ряда при и .

Если , то получим - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. .

Если , то получим - числовой знакочередующийся ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. .

Итак, область абсолютной сходимости исходного функционального ряда - .

II способ.

Определим и заданного ряда: , .

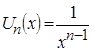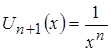По признаку Даламбера абсолютной сходимости функционального ряда можно записать:

.

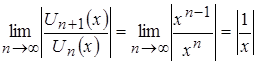Если , т.е. , то заданный функциональный ряд сходится абсолютно.

Исследуем на сходимость исходный функциональный ряд при и .

Если , то получим - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е.

Если , то получим - числовой знакочередующийся ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. .

Ответ: область абсолютной сходимости исходного функционального ряда - .

Пример №4 (№339 из, с комментариями преподавателя).

Найти область сходимости функционального ряда:

.

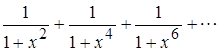Решение

Найдем общий элемент заданного функционального ряда . Если , то ; Так как , то ряд расходится.

Образование, педагогика, воспитание:

Реализация условий использования эвристической технологии в образовательном процессе
Рассмотрим некоторые виды уроков, которые можно провести в качестве эвристических. Творческие лаборатории Структура уроков при эвристическом обучении предполагает организацию творческой, поисковой математической деятельности учащихся с различным уровнем учебных и математических способностей. Диффер ...

Основные нормативно-правовые акты по правам ребенка в Российском законодательстве
Конституция Российской Федерации и права ребенка Основным правовым актом в нашей стране является принятая 12 декабря 1993 года Конституция Российской Федерации. В главе "Права человека" Конституции закреплены отвечающие духу и букве международных договоров и соглашений, заключенных Россие ...

Параметры, позволяющие диагностировать развитие креативности в процессе музыкального школьного образования
Креативность является научно установившейся категорией в психологической науке. Основная задача психологии творчества состоит в раскрытии психических закономерностей и механизмов творческого процесса и креативности (творческости). Творчество рассматривается как основа и механизм развития психики. ( ...