Электронное пособие по теме “Функциональные последовательности и ряды"

Итак, сумма функционального ряда при равна .

Ответ: При .

Пример №9 (№16 из [10], студент у доски с помощью преподавателя).

Найти сумму ряда:

.

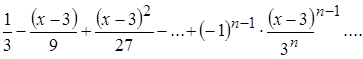Решение

По признаку Даламбера абсолютной сходимости функционального ряда можем записать:

.

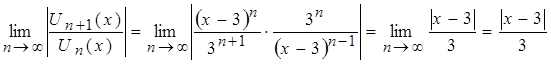В соответствии с признаком Даламбера, если 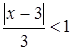, т.е. или , то заданный функциональный ряд сходится абсолютно.

Если 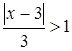, т.е. , исследуемый функциональный ряд расходится.

При получается числовой положительный ряд . Он расходится, так как не выполняется необходимое условие сходимости числового ряда, т.е. . Следовательно, исследуемый функциональный ряд в точке расходится.

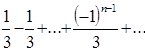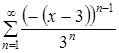При получается числовой знакочередующийся ряд вида . Он расходится, так как не удовлетворяет условиям признака Лейбница: а) ; б) . Значит, в точке функциональный ряд расходится.

Следовательно, областью сходимости заданного функционального ряда является интервал .

Найдем сумму заданного функционального ряда на его области сходимости. Если , то ряд представляет собой сумму убывающей геометрической прогрессии с . Сумма ряда 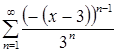на интервале будет определяться по формуле

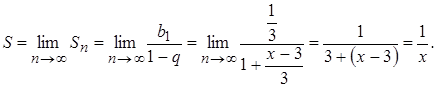
Ответ: При .

В конце занятия подводятся итоги. Преподавателю целесообразно предложить студентам описать алгоритмы выполнения заданий каждого рассмотренного типа, особенности заданий каждого типа, их взаимосвязь. Ниже приведены алгоритмы выполнения рассмотренных заданий.

Исследование ряда на сходимость в точке

Вместо переменной в функциональный ряд подставляется ее значение.

Исследуется полученный числовой ряд на сходимость с помощью признаков сходимости числовых рядов.

Формулируется вывод о сходимости исследуемого функционального ряда в заданной точке.

Определение области сходимости функционального ряда

Определение интервала сходимости функционального ряда (ряд исследуется на всей числовой прямой).

Исследование ряда на сходимость на концах интервала сходимости (сходимость функционального ряда в точке).

Образование, педагогика, воспитание:

Роль семьи в воспитании ребёнка
Современный мир с его экономическими кризисами, увеличением числа разводов, ухудшением качества образования, постоянными стрессами и прочими «прелестями» цивилизации истощает людей физически, эмоционально и духовно, поэтому им все труднее воспитывать нас, детей. Именно мы, наиболее уязвимые и больш ...

Познавательное развитие детей в ДОУ
Накопленные к шести годам сведения о большом мире является серьезной базой для дальнейшего развития познавательной сферы ребенка. Эта база данных о большом мире требует от него определенных умений и упорядочивания накопленных и поступающих сведений. Процесс знаний направлен на: - содержательное упо ...

Особенности культурного воспитания детей старшего дошкольного возраста в ДОУ
В условиях духовного возрождения общества, роста его национального самосознания закономерен интерес к освоению культурного пространства как корневой системе, питающей современное общество, способствующей духовному оздоровлению всего народа. Не случайно так остро встал вопрос необходимости гуманизац ...