Электронное пособие по теме “Функциональные последовательности и ряды"

Можно провести письменную самостоятельную работу по домашнему заданию на 15 минут. В самостоятельной работе предлагается 2 варианта, в каждом варианте по 3 задания. Например, Вариант №1: №№ 2, 11, 14; Вариант№2: №№ 3, 12, 15. Преподаватель самостоятельно определяет какие задания и в какой последовательности будут содержать каждый из вариантов. Во время проведения самостоятельной работы у доски работают студенты, которым предлагаются наиболее сложные на взгляд преподавателя примеры. Например, №№ 13,10. По завершении самостоятельной работы эти примеры проверяются аудиторией.

Преподаватель: А теперь давайте вспомним определения и формулировки теорем по теме "Равномерная сходимость функциональных последовательностей и рядов", необходимые нам сегодня для выполнения упражнений.

Проводится фронтальный опрос с целью проверки теоретических знаний по изучаемой теме. Студентам предлагается отвечать на следующие вопросы у доски, выполняя необходимые при ответе записи. К доске вызываются сразу 3-4 студента.

Вопрос 1: Какая последовательность называется равномерно сходящейся?

Ответ: Определение №1. Функциональная последовательность называется равномерно сходящейся на множестве , если существует функция , в которой она равномерно сходится на множестве . Обозначение:

[14].

Вопрос 2: Какой функциональный ряд называется равномерно сходящимся? Сформулировать определение такого ряда, используя понятие последовательности его частичных сумм.

Ответ: Определение №2. Если последовательность частичных сумм функционального ряда равномерно сходится к функции на множестве , то ряд равномерно сходится на множестве [21].

Вопрос 3: Дать определение равномерно сходящегося функционального ряда, используя понятие остатка функционального ряда.

Ответ: Определение №3. Представим сумму функционального ряда в виде: , где [-остаток функционального ряда].

Определение №4. Сходящийся функциональный ряд 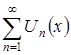называется равномерно сходящимся в некоторой области , если для каждого сколь угодно малого числа найдется такое положительное число , что при выполняется неравенство для любого из области . При этом сумма равномерно сходящегося ряда 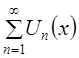в области , где (n=1,2,3…) - непрерывные функции в области , есть непрерывная функция.

Образование, педагогика, воспитание:

Этнопедагогические традиционные методы семейного физического воспитания Якутов
В последнее время в Республике Саха (Якутия) сделано немало для сохранения и возрождения духовных, культурных ценностей, накопленных на протяжении жизни многих поколений народа Саха. Традиционный образ жизни, жизнь в гармонии с природой - это не только прошлое человечества, но в значительной его ча ...

Цели и задачи профильного обучения
В наше время одним из важнейших направлений модернизации системы образования в России остаётся переход к старшей профильной школе. Необходимость перехода старшей ступени на профильное обучение определена Правительством России в «Концепции модернизации российского образования на период до 2010 года» ...

Особенности формирования и развития познавательного интереса школьников
Организация деятельности учащихся включает в себя постановку учебной задачи перед учащимися и создание благоприятных условий для ее выполнения. Современная дидактика рекомендует правила выдвижения познавательных задач: познавательная задача должна вытекать из предметного содержания, чтобы сохраняла ...