Электронное пособие по теме “Функциональные последовательности и ряды"

Решение

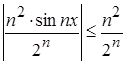Так как , то при .

Ряд - мажорантный, исследуем его на сходимость. По признаку Даламбера имеем:

.

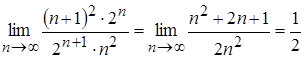Так как , то ряд сходится. По теореме Вейерштрасса, так как для R 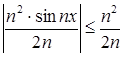, то заданный ряд 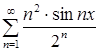сходится равномерно и абсолютно на промежутке .

Ответ: Заданный ряд сходится абсолютно и равномерно на интервале .

Пример №26 (№354 из [7]).

Исследовать на равномерную сходимость ряд 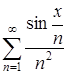на всей числовой оси.

Решение

Воспользуемся признаком Вейерштрасса равномерной и абсолютной сходимости функциональных рядов. Так как при любом , то справедливо неравенство 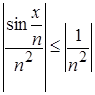, при R. 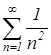- сходящийся ряд Дирихле с . Значит, и ряд 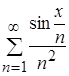сходится абсолютно и равномерно при R.

Ответ: Заданный ряд сходится абсолютно и равномерно при R.

Пример №27 (№76 из [10])

Показать, что ряд 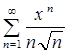сходится равномерно на отрезке

Решение

Так как при 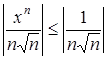, и ряд 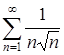- сходящийся ряд Дирихле с , то, по признаку Вейерштрасса, ряд 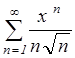сходится абсолютно и равномерно на отрезке .

Ответ: Заданный ряд сходится абсолютно и равномерно на отрезке .

Пример №28 (№82 из [10]).

Сходится ли равномерно ряд 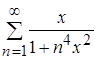, если ?

Решение

Если , то 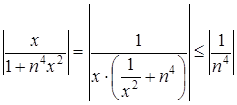. Так как -сходящийся числовой положительный ряд - ряд Дирихле с , то по теореме Вейерштрасса, ряд сходится абсолютно и равномерно при .

Ответ: Заданный ряд сходится абсолютно и равномерно при .

Образование, педагогика, воспитание:

Возрастное психофизическое развитие ребенка и его особенности
В процессе жизни человек все время развивается, то есть изменяется в количественном и качественном отношении. При этом можно особо говорить о развитии организма человека: физическом, умственном, психическом, личностном; а также о развитии многих других его качеств и особенностей. Развитие человека ...

Роль картинки в развитии речи детей дошкольного возраста
Особую роль картинки в развитии ребенка и в развитии речи детей дошкольного возраста отводила Е.И. Тихеева. Она описала что картинам как фактору умственного развития ребенка должно быть отведено почетное место с первых лет его жизни. Мы знаем, какое громадное значение имеют опыт и личное наблюдение ...

Основные принципы внеклассной работы
Условием успешной реализации регионального компонента образованием является его кадровое и научно - методическое обеспечение. Способность учителя связать базовый (федеральный) компонент содержания образования с особенностями региона, его исторической, географической, экономической, социальной, экол ...