Электронное пособие по теме “Функциональные последовательности и ряды"
Значит, к ряду 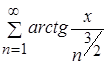 можно применить теорему о почленном дифференцировании.
можно применить теорему о почленном дифференцировании.
Ответ: Теорему о почленом дифференцировании применить можно.
Пример №31 (№108 из [10], студент самостоятельно)
Убедиться, что ряд 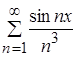 можно дифференцировать почленно.
можно дифференцировать почленно.
Решение
Члены функционального ряда 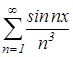 являются непрерывно дифференцируемыми функциями при
являются непрерывно дифференцируемыми функциями при ![]() R.
R.
Очевидно неравенство ![]() при
при ![]() R,
R, ![]() N.
N.
Сравним функциональный и числовой ряды 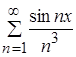 и
и 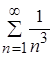 .
.
При ![]() R,
R, ![]() N справедливо неравенство
N справедливо неравенство 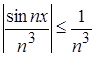 .
.
Числовой положительный ряд 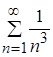 является сходящимся рядом, так как представляет собой ряд Дирихле с
является сходящимся рядом, так как представляет собой ряд Дирихле с ![]() .
.
Значит, по признаку Вейерштрасса, функциональный ряд 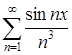 сходится равномерно и абсолютно при
сходится равномерно и абсолютно при ![]() R.
R.
Найдем производную общего элемента заданного функционального ряда: 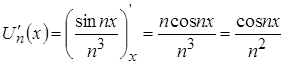 при
при ![]() R.
R.
Составим функциональный ряд из производных членов функционального ряда 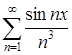 :
:
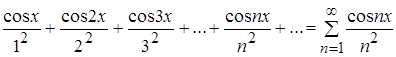 .
.
Члены этого функционального ряда являются непрерывными функциями при ![]() R.
R.
Кроме того, функциональный ряд 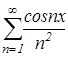 абсолютно и равномерно сходится при
абсолютно и равномерно сходится при ![]() R в соответствии с признаком Вейерштрасса. Действительно, так как
R в соответствии с признаком Вейерштрасса. Действительно, так как
a) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 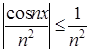 при
при ![]() R;
R;
в) ![]() числовой положительный сходящийся ряд (ряд Дирихле с
числовой положительный сходящийся ряд (ряд Дирихле с ![]()
![]() ).
).
Значит, к заданному функциональному ряду 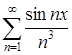 можно применить теорему о почленном дифференцировании.
можно применить теорему о почленном дифференцировании.
Ответ: Можно почленно дифференцировать заданный функциональный ряд.
Преподаватель: А теперь рассмотрим задания на возможность интегрируемости ряда.
Пример №32 (№344 из [7], с комментариями преподавателя).
Законно ли применение к ряду
![]()
теоремы об интегрировании функциональных рядов в промежутках ![]() ?
?
Решение
Для того, чтобы функциональный ряд можно было почленно проинтегрировать на отрезке, необходимым является непрерывность его членов и равномерная сходимость ряда на этом промежутке.
Образование, педагогика, воспитание:
Компетентностный подход в подготовке специалиста. Государственный
образовательный стандарт 3-го поколения
Учебные цели 1. Знать основные структурные компоненты педагогического процесса в вузе. 2. Знать специфику понятий – компетенция и компетентность, 3. Иметь представление об истории и особенностях компетентностного подхода в профессиональном образовании Отводимое время – 2 часа План лекции 1. Совреме ...
Типы современного урока истории
В современной педагогической науке выделяют следующие наиболее общепринятые типы уроков: уроки новых знаний; уроки анализа и синтеза знаний; уроки формирования навыков и умений; уроки диагностики знаний, навыков и умений. Рассмотрим каждый из типов занятий и входящие в них формы и виды уроков. 1. У ...
Справочная и научно-популярная литература и
методика их использования. Учебное оборудование по математике и методика
использования его в учебной работе
Обучение пользованию справочниками по математике, справочными таблицами и другой справочной литературой должно найти своё место при изучении математики в средней школе. Справочники необходимы по той причине, что для запоминания выбирается первостепенное, необходимое для изучения дальнейшего курса, ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

