Электронное пособие по теме “Функциональные последовательности и ряды"
Элементы заданного функционального ряда являются непрерывными функциями при ![]() R, значит, они будут непрерывными и на отрезке
R, значит, они будут непрерывными и на отрезке ![]() , ведь
, ведь ![]() .
.
Исходный ряд 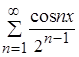 равномерно и абсолютно сходится при
равномерно и абсолютно сходится при ![]() R по признаку Вейерштрасса, а, значит, и на отрезке
R по признаку Вейерштрасса, а, значит, и на отрезке ![]() , так как:
, так как:
a) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 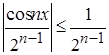 при
при ![]() R;
R;
в) 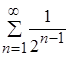 - числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии:
- числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии: 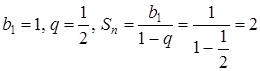 ).
).
Следовательно, к заданному функциональному ряду 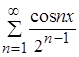 можно применить теорему о почленном интегрировании ряда на отрезке
можно применить теорему о почленном интегрировании ряда на отрезке ![]() .
.
Ответ: Теорему применить можно.
Пример №33 (№114 из [7], студент с помощью преподавателя).
Показать, что ряд 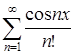 допускает почленное интегрирование на отрезке
допускает почленное интегрирование на отрезке ![]() , написать полученный при этом ряд.
, написать полученный при этом ряд.
Решение
Функциональный ряд 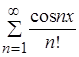 можно интегрировать почленно на отрезке
можно интегрировать почленно на отрезке ![]() , если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
, если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
Элементы функционального ряда 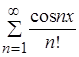 являются непрерывными функциями для
являются непрерывными функциями для ![]() R, значит, и на отрезке
R, значит, и на отрезке ![]() .
.
Кроме того, по признаку Вейерштрасса заданный функциональный ряд равномерно и абсолютно сходится на R, а, значит, и на отрезке ![]() . Действительно, так как:
. Действительно, так как:
а) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 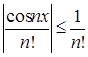 при
при ![]() R;
R;
в) ![]() - числовой положительный сходящийся ряд. По признаку Даламбера:
- числовой положительный сходящийся ряд. По признаку Даламбера: 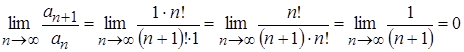 , 0<1.
, 0<1.
Значит, теорему о почленном интегрировании к функциональному ряду 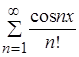 на отрезке
на отрезке ![]() применить можно.
применить можно.
Проинтегрируем почленно заданный ряд на отрезке ![]() .
.
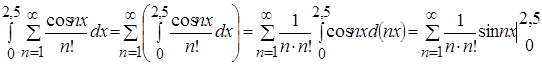 .
.
Ряд, полученный от почленного интегрирования заданного функционального ряда имеет вид 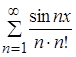 на
на ![]() .
.
Ответ: 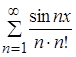 при
при ![]() .
.
Образование, педагогика, воспитание:
Система образования Канады
Канада относится к числу государств, дипломы которых котируются во всем мире. Это неудивительно: Канада расходует на развитие системы образования больше средств, чем многие другие развитые страны. Канада является одним из мировых лидеров в области высоких технологий, аэрокосмической индустрии, микр ...
Изучение народного искусства в начальной школе на уроках изобразительного
искусства; влияние русской народной игрушки на формирование личности ребенка
В настоящее время многие аспекты освоения народного и декоративно- прикладного искусства в школе изучены достаточно полного и глубоко. Аспекты освоения народного искусства у школьников происходит на уроках декоративного рисования Содержание художественного – эстетического образования, основанное на ...
Гражданская активность и особенности ее формирования у учащихся школы
надомного обучения
В настоящее время в России на государственном уровне признано, что гражданско-правовое образование является одним из приоритетных направлений образовательной политики. Существует программа воспитания демократической гражданственности и образования в области прав человека, принятая Советом Европы 15 ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

