Электронное пособие по теме “Функциональные последовательности и ряды"

Вопрос 2: Как звучит теорема об интегрировании функциональной последовательности? Сформулируйте условие интегрируемости функционального ряда.

Ответ: Теорема 2. Если последовательность функций , непрерывных на , сходится равномерно на указанном отрезке к функции , то для последовательность определенных интегралов с переменным верхним пределом 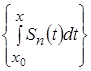будет сходиться равномерно на к определенному интегралу 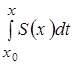, причем будет справедлива формула:

.

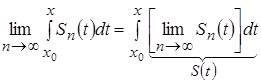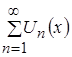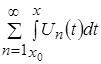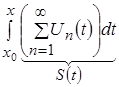Следствие. Пусть функции , N непрерывны на и функциональный ряд равномерно сходится на указанном отрезке. Тогда для функциональный ряд вида будет равномерно сходиться на отрезке к или к 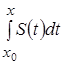, т.е. функциональный ряд можно почленно интегрировать:

.

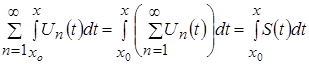Вопрос 3: Как звучат теорема о почленном дифференцировании функциональных последовательностей и рядов?

Ответ: Теорема 4. Пусть последовательность функций , непрерывно дифференцируемых на , и последовательность их производных равномерно сходятся на указанном отрезке. Тогда предел последовательности непрерывно диффепенцируемых функций непрерывно дифференцируем на указанном отрезке и верно равенство:

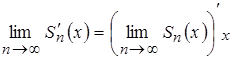или.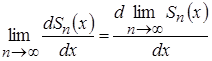

Следствие. Пусть функции непрерывно дифференцируемы на и функциональные ряды: 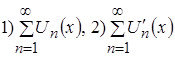равномерно сходятся на . Тогда сумма функционального ряда 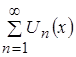непрерывно дифференцируема на указанном отрезке и верно равенство:

=.

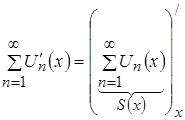Преподаватель: Итак, а теперь приступим непосредственно к выполнению упражнений.

При объяснении нового материала, на экран телевизора выводится задание с подробным решением, преподаватель комментирует решение, студенты записывают в тетради.

При объяснении материала следует обратиться к технологической карте по теме "Функциональные последовательности и ряды" [16], в которой отмечены затруднения при изучении данной темы, а также типичные ошибки, допускаемые студентами.

Образование, педагогика, воспитание:

Определения равномерно сходящихся функциональных последовательностей и рядов
Опр.5. Последовательность функций равномерно сходится на множестве Х к предельной функции , если . Опр.6. Функциональная последовательность называется равномерно сходящейся на множестве X, если существует функция , в которой она равномерно сходится на множестве X. Обозначение: . Геометрический смыс ...

Почленное дифференцирование функциональных рядов
Теорема 7. Пусть последовательность функций , непрерывно дифференцируемых на , и последовательность их производных равномерно сходятся на , тогда предел последовательности непрерывно дифференцируемых функций , т.е. , непрерывно дифференцируем на указанном отрезке и верно равенство: или . Доказатель ...

Практика диагностики и формирования культурно-гигиенических навыков у детей младшего дошкольного возраста
Исследовательская работа проводится в виде эксперимента с детьми младшей группы детского центра « Волшебный фонарик», г. Москвы, в течение июня по декабрь 2013 года. В работе принимали участие 10 детей в возрасте 3-4 лет. Нами были определены задачи экспериментальной части исследования: Изучить усл ...