Электронное пособие по теме “Функциональные последовательности и ряды"
Ответ: Доказана равномерная и абсолютная сходимость на интервале ![]() .
.
Пример №21 (№164 из [8], студент самостоятельно у доски).
Исследовать на равномерную сходимость ряд 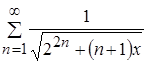 на интервале
на интервале ![]() .
.
Решение
Если ![]() , то
, то 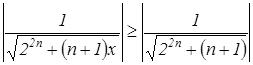 - условие равномерной сходимости не выполняется.
- условие равномерной сходимости не выполняется.
Если ![]() , то
, то 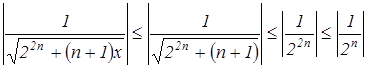 . Ряд
. Ряд ![]() мажорантный по отношению к ряду
мажорантный по отношению к ряду 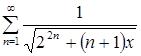 . По признаку Даламбера сходимости числовых рядов имеем:
. По признаку Даламбера сходимости числовых рядов имеем: 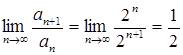 . Так как
. Так как ![]() , то числовой ряд сходится. Значит, по теореме Вейерштрасса равномерно сходимости функциональных рядов, так как
, то числовой ряд сходится. Значит, по теореме Вейерштрасса равномерно сходимости функциональных рядов, так как 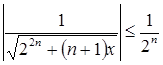 при
при ![]() , ряд
, ряд 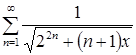 сходится равномерно и абсолютно.
сходится равномерно и абсолютно.
Ответ: Равномерно и абсолютно сходится при ![]() .
.
Преподаватель: Доказательство равномерной сходимости может быть и вспомогательной задачей, которую необходимо решить, чтобы выполнить основное задание.
Пример №22 (№94 из [10], с комментариями преподавателя).
Показать, что на луче ![]() функциональный ряд
функциональный ряд
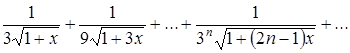
равномерно сходится. Начиная с какого номера ![]() , остаток ряда
, остаток ряда ![]() (независимо от значения
(независимо от значения ![]() ) удовлетворяет неравенству
) удовлетворяет неравенству ![]() ?.
?.
Решение
Воспользуемся признаком Вейерштрасса.
Так как при ![]() справедливо неравенство:
справедливо неравенство: ![]() , то элементы заданного функционального ряда на указанном промежутке не больше соответствующих членов положительного числового ряда
, то элементы заданного функционального ряда на указанном промежутке не больше соответствующих членов положительного числового ряда ![]() , т.е.
, т.е. 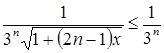 при
при ![]() .
.
Числовой положительный ряд ![]() сходится, так как представляет собой сумму убывающей геометрической прогрессии с
сходится, так как представляет собой сумму убывающей геометрической прогрессии с
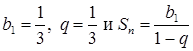 ,
, 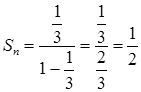 ,
, ![]() .
.
Значит, функциональный ряд 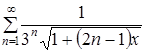 сходится равномерно и абсолютно при
сходится равномерно и абсолютно при ![]() .
.
Для оценки остатка ![]() заданного функционального ряда подсчитаем остаток
заданного функционального ряда подсчитаем остаток ![]() числового положительного (мажорантного) ряда:
числового положительного (мажорантного) ряда:
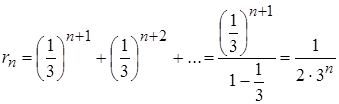 , где
, где 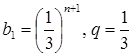 .
.
Образование, педагогика, воспитание:
Методические требования к художественным текстам для домашнего чтения на
старшей стадии обучения учащихся иностранному языку
Для успешной организации процесса обучения самостоятельному чтению представляется важным рассмотреть требования к текстам. Основу типологической общности текстового материала для домашнего чтения на средней стадии обучения иностранному языку, на наш взгляд должны составлять требования к: 1) жанру, ...
Неурочные формы внеклассной работы
Спортивные соревнования являются одной из самых интересных, увлекательных форм внеклассной работы по физическому воспитанию в начальной школе. Они содействуют привлечению учащихся к систематическим занятиям физическими упражнениями дома и в коллективе физкультуры, повышают физическую подготовленнос ...
Изучение народного искусства в начальной школе на уроках изобразительного
искусства; влияние русской народной игрушки на формирование личности ребенка
В настоящее время многие аспекты освоения народного и декоративно- прикладного искусства в школе изучены достаточно полного и глубоко. Аспекты освоения народного искусства у школьников происходит на уроках декоративного рисования Содержание художественного – эстетического образования, основанное на ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

