Электронное пособие по теме “Функциональные последовательности и ряды"

Значит, заданный ряд 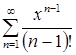равномерно и абсолютно сходится при .

Ответ: Доказана равномерная и абсолютная сходимость при .

Пример №18 (№89 из [10], c комментариями преподавателя).

С помощью признака Вейерштрасса показать, что ряд

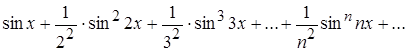
сходится равномерно в промежутке .

Решение

Так как 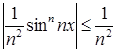при R и числовой положительный ряд сходится, как обобщенный гармонический ряд с , то заданный функциональный ряд сходится равномерно и абсолютно при любых значениях .

Ответ: Доказана равномерная и абсолютная сходимость для R.

Пример №19 (№79 из [10], студент с помощью преподавателя).

Показать, что ряд 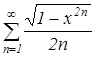сходится равномерно на отрезке .

Решение

Если , то . Значит, числовой положительный ряд 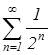является мажорантным. По признаку Даламбера абсолютной сходимости числовых рядов имеем: 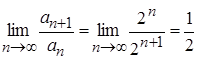, так как , то числовой ряд сходится абсолютно.

Следовательно, по теореме Вейерштрасса равномерной и абсолютной сходимости функциональных рядов, ряд 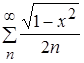сходится при равномерно и абсолютно.

Если , то ряд примет вид - сходится. Значит, и заданный функциональный ряд сходится равномерно.

Если , то ряд примет вид - сходится. Значит, и заданный функциональный ряд сходится равномерно.

Итак, ряд 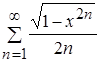сходится равномерно и абсолютно на отрезке .

Ответ: Доказана равномерная и абсолютная сходимость на отрезке . Пример №20 (№52 из [10], студент самостоятельно у доски).

Исследовать на равномерную сходимость ряд на всей числовой оси.

Решение

Так как при N и R, то в качестве мажорантного ряда выберем - числовой положительный ряд (ряд Дирихле). Он сходится. Следовательно, и ряд 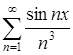по теореме Вейерштрасса равномерно и абсолютно сходится, так как 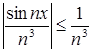при R

Образование, педагогика, воспитание:

Фонетические факторы внятности
Наряду с общими требованиями к внятности и членораздельности, следует иметь в виду и ряд вытекающих из них частных требований, касающихся разных сторон фонетического оформления речи, а именно: голоса, фонетического облика слова (включая их фонематический состав, слоговый ритм, ударение, орфоэпию), ...

Работа с кадрами дошкольного учреждения
Современная практика работы дошкольных учреждений показывает, что далеко не все педагоги и родители знают особенности психофизического, эмоционального и интеллектуального развития ребенка-дошкольника и, как следствие, слабо владеют приемами здоровьесберегающей педагогики. Для более эффективного вза ...

Общие требования по организации рабочего места учителя
Согласно требованиям ГОСТ 22046-89 мебель для организации рабочего места учителя должна включать: стол с местом для аппаратуры графопроектора и компьютера, тумбу для принтера, стул, классную доску. Современная школа предъявляет к оснащению рабочего места учителя новые требования. Это автоматизирова ...