Электронное пособие по теме “Функциональные последовательности и ряды"

Пример №29 (№86 из [10]).

Показать, что ряд сходится равномерно на интервале .

Решение

Так как 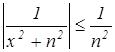при любом R и ряд - сходящийся числовой положительный ряд - ряд Дирихле с , то ряд 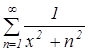по признаку Вейерштрасса, сходится абсолютно и равномерно на интервале .

Ответ: Заданный ряд сходится абсолютно и равномерно при .

Практическое занятие №3

Тема: "Интегрирование и дифференцирование функциональных

последовательностей и рядов"

Тип занятия: практикум решения задач.

Форма занятия: комбинированная между коллективной и фронтальной.

Средства обучения на занятии: сборник задач, методические рекомендации к практическим занятиям, телевизор, подключенный к компьютеру, графопроектор, доска, мел.

Цель: закрепление знаний полученных на лекции, применение их на практике.

Методы: словесные, наглядные, по дидактической цели - познавательные, по характеру познавательной деятельности - проблемные.

Ход занятия:

Организационная часть: Студентам сообщается тема практического занятия, его цель, проверка присутствующих (3 минуты).

2. Основная часть: Проверка домашнего задания (12 минут). Фронтальный опрос по изученной теме (10 минут). Ознакомление с новым материалом, первичное закрепление и осмысление (60 минут). Подведение итогов и постановка домашнего задания. (5 минут).

Конспект занятия

Преподаватель: Тема занятия: "Интегрирование и дифференцирование функциональных последовательностей и рядов". Цель - приобрести навыки решения задач по вышеуказанной теме. Но прежде, проведем самостоятельную работу, которая позволит определить, насколько успешно вы справились с домашним заданием.

Проводится самостоятельная работа по домашнему заданию на 15 минут. В самостоятельной работе предлагается 3 варианта, в каждом варианте по 2 задания. Например, Вариант №1: №№ 23, 26; Вариант №2: №№ 24, 27, Вариант №2: №№ 21,28. Преподаватель самостоятельно определяет какие задания и в какой последовательности будут содержать каждый из вариантов. Во время проведения самостоятельной работы у доски работают студенты, которым предлагаются наиболее сложные на взгляд преподавателя примеры. Например, №№ 29, 25. По завершении самостоятельной работы эти примеры проверяются аудиторией.

Преподаватель: А теперь давайте вспомним определения и формули-ровки теорем по теме "Интегрирование и дифференцирование функциональных последовательностей и рядов", необходимые нам сегодня для решения упражнений.

Проводится фронтальный опрос с целью проверки теоретических знаний по изучаемой теме. Студентам предлагается отвечать на следующие вопросы у доски, выполняя необходимые при ответе записи. К доске вызываются сразу 3-4 студента.

Вопрос 1:. Сформулируйте теорему о непрерывности суммы функционального ряда в точке.

Ответ: Теорема 1. Если функции непрерывны в точке , и функциональный ряд 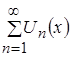равномерно сходится на множестве , то его сумма также непрерывна в точке .

Образование, педагогика, воспитание:

Технология педагогического взаимодействия как условие эффективной педагогической деятельности
Педагогическое общение – специфическая форма общения, имеющая свои особенности и в то же время подчиняющаяся общим психологическим закономерностям, присущим общению как форме взаимодействия человека с другими людьми, включающей коммуникативный, интерактивный и перцептивный компоненты. Педагогическо ...

Основные требования к отбору задач для занятий элективного курса
Элективный курс по математике представляет собой одну тему, рассмотренную глубоко (например, элективный курс может называться «Комбинаторные задачи», а может состоять из нескольких тем, связанных друг с другом (например, «Элементы комбинаторики, статистики и теории вероятностей»). Основной курс мат ...

Понятие "эвристическая технология" в психолого-педагогической литературе
Термин "эвристика" происходит от греческого heuresko - отыскиваю, открываю. В настоящее время используется несколько значений этого термина. Эвристика может пониматься как: 1) научно-прикладная дисциплина, изучающая творческую деятельность (в то же время следует признать, что основателей ...