Электронное пособие по теме “Функциональные последовательности и ряды"

Преподаватель: Теоремы о почленном интегрировании и дифференцировании можно использовать при нахождении суммы ряда.

Пример №34 (№ 112 из [8], студент у доски с помощью преподавателя).

Найти сумму ряда , продифференцировав почленно ряд

Решение

Почленно продифференцировать функциональный ряд возможно, если члены ряда и производные его членов непрерывны, а сам ряд и ряд составленный из производных членов его ряда, сходится равномерно на данном промежутке.

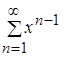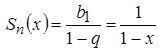Функциональный ряд представляет собой сумму убывающей геометрической прогрессии при , т.е. при , где при . Значит, сумма ряда при .

Следовательно, функциональный ряд 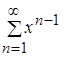сходится к при . Члены ряда 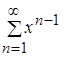являются непрерывными функциями при R.

Осталось доказать, что функциональный ряд 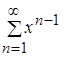равномерно сходится на промежутке .

Для можно найти такое , что .

По признаку Даламбера сходимости положительных числовых рядов получим 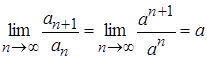. А так как , то и, значит, числовой ряд сходится.

Значит, по признаку Вейерштрасса будет равномерно и абсолютно сходиться функциональный ряд 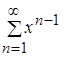на промежутке .

Следовательно, функциональный ряд 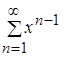на промежутке можно почленно продифференцировать:

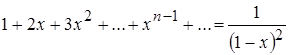, , т.е. сумма функционального ряда 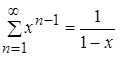непрерывно дифференцируема.

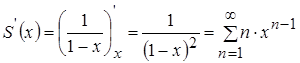при .

Ответ: 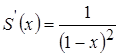при .

Пример №35 (№113 из [10], студент у доски с помощью преподавателя).

Найти сумму ряда .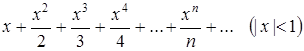

Решение

По признаку Даламбера абсолютной сходимости функциональных ря-дов имеем: 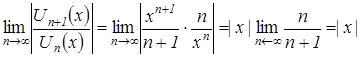. Если , т.е. , то заданный функциональный ряд сходится абсолютно. Так как ряд сходится, то его остаток оценивается с помощью неравенства , т.е. 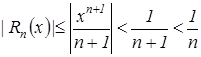. Неравенства и равносильны, значит, взяв , где - какое-нибудь целое положительное число, которое удовлетворяет условию , приходим к неравенству .

Образование, педагогика, воспитание:

Методологические основы применения информационных технологий в процессе преподавания информатики в начальной школе
Наше время характерно стремительным развитием информационных и компьютерных технологий, которые существенно перестраивают практику повседневной жизни. Сегодня ребенок живет уже в мире отличном от того, в котором выросли его родители. Эти тенденции проявляются и в образовании. Образование на совреме ...

Методические рекомендации для воспитателей по формированию культурно-гигиенических навыков у детей младшего дошкольного возраста
Проведя наше исследование, мы считаем, что в каждом детском саду должны проводиться специальные занятия или мероприятия, направленные на формирование культурно - гигиенических навыков у детей младшего дошкольного возраста. Заложенные в детстве навыки и привычки сохраняются у дошкольников на всю ост ...

Коммуникативно-прагматическая модель обучения английскому языку
Формирование межкультурной компетенции – это один из самых актуальных вопросов современной российской теории и практики обучения иностранному языку, так как выступает одной из важнейших целей мультикультурного образования и предусматривает наличие: –достаточной информированности о культурной специф ...