Электронное пособие по теме “Функциональные последовательности и ряды"
Действительно, так как:
а) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 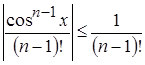 для
для ![]() R;
R;
в) 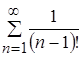 - числовой положительный сходящийся ряд. По признаку Даламбера
- числовой положительный сходящийся ряд. По признаку Даламбера 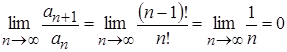 , 0<1.
, 0<1.
Значит, теорему о почленном интегрировании к функциональному ряду 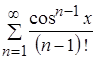 на отрезке
на отрезке ![]() применить можно.
применить можно.
Ответ: Можно почленно проинтегрировать функциональный ряд 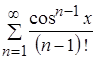 .
.
Пример №37 (№106 из [10]).
Дифференцируя прогрессию 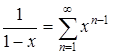 получить новые разложения. Решение
получить новые разложения. Решение
Ряд 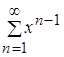 сходится на интервале
сходится на интервале ![]() , как сумма убывающей геометрической прогрессии. Производная общего члена заданного функционального ряда примет вид:
, как сумма убывающей геометрической прогрессии. Производная общего члена заданного функционального ряда примет вид: ![]() . Составим ряд из производных:
. Составим ряд из производных:
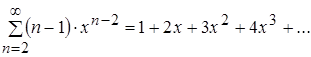 .
.
Исследуем полученный ряд на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
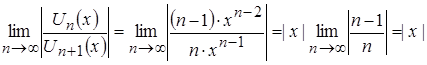 ,
,
если ![]() , т.е.
, т.е. ![]() , то ряд
, то ряд 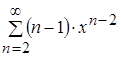 сходится абсолютно.
сходится абсолютно.
Ответ: При дифференцировании заданной прогрессии получен ряд 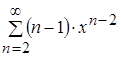 .
.
Пример №38 (№109 из [10]).
Убедиться, что ряд 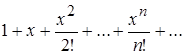 можно продифференцировать почленно.
можно продифференцировать почленно.
Решение
Исследуем заданный функциональный ряд на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
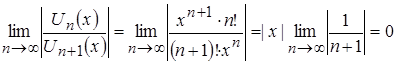 ,
,
Так как ![]() , то ряд
, то ряд ![]() сходится абсолютно при
сходится абсолютно при ![]() R. Тогда остаток ряда можно оценить с помощью неравенства
R. Тогда остаток ряда можно оценить с помощью неравенства ![]() , т.е.
, т.е.
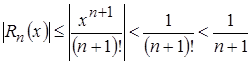 .
.
Так как неравенства ![]() и
и ![]() равносильны, то, взяв
равносильны, то, взяв ![]() , где
, где ![]() - какое-нибудь целое положительное число, удовлетворяющее условию
- какое-нибудь целое положительное число, удовлетворяющее условию ![]() , приходим к неравенству
, приходим к неравенству ![]() . Итак, заданный функциональный ряд сходится абсолютно и равномерно при
. Итак, заданный функциональный ряд сходится абсолютно и равномерно при ![]() R. Члены ряда являются непрерывными функциями при
R. Члены ряда являются непрерывными функциями при ![]() R.
R.
Производная общего члена заданного функционального ряда примет вид:
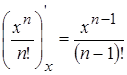 .
.
Образование, педагогика, воспитание:
Электронное
пособие по теме “Функциональные последовательности и ряды"
В процессе выполнения данной выпускной квалификационной работы было создано электронное пособие по теме "Функциональные последовательности и ряды". Обучающая часть пособия представлена в формате HTML, а контролирующая - на языке DELFI. При создании обучающей программы пособия (совокупност ...
Роль словесного ударения
Данная методика и приемы работы взяты из разработок К.А. Волковой, Ф.Ф. Рау, Н.Ф. Слезиной. Словесное ударение является одним из трех элементов фонетической системы русского языка. Оно вместе с числом слогов, является носителем его ритма. Благодаря ударению осуществляется выделение слов в речи, а т ...
Постановка проблемы в психолого-педагогической литературе
Русский историк Н.И. Караев писал: «История есть, между прочим, и история деятельности людей…». Таким образом, автор нацеливал учащихся средней школы на необходимость глубокой проработки знаний о жизни и деятельности исторических личностей. Поскольку наши исследования были посвящены урокам истории ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

