Электронное пособие по теме “Функциональные последовательности и ряды"

Итак, заданный функциональный ряд сходится равномерно и абсолютно в промежутке .

Кроме того, члены заданного функционального ряда являются непрерывными функциями R.

Найдем производную общего члена заданного функционального ряда: 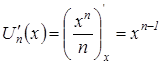. Исследуем функциональный ряд 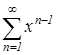на абсолютную и равномерную сходимость. Для можно найти такое , что . По признаку Даламбера сходимости числовых рядов имеем: 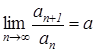, так как , то числовой ряд сходится абсолютно.

Значит, по признаку Вейерштрасса равномерной сходимости функциональных рядов, ряд 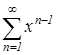сходится равномерно и абсолютно при .

Следовательно, заданный функциональный ряд можно почленно продифференцировать.

Продифференцируем почленно заданный функциональный ряд 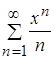и получим такой функциональный ряд:

.

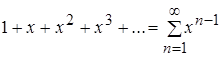Полученный ряд при представляет собой сумму убывающей геометрической прогрессии с .

Тогда и при .

Итак, сумма ряда при , т.е. .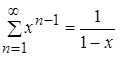

Функциональный ряд 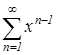равномерно и абсолютно сходится при , и функция непрерывна при . Значит, ряд 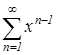можно почленно интегрировать. Проинтегрировав в пределах от до , находим

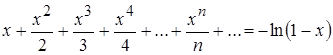при .

Ответ: при .

В конце занятия подводятся итоги, выставляются оценки, оговаривается домашнее задание.

Преподаватель: Итак, подведем итог: на сегодняшнем занятии мы с вами научились исследовать функциональные ряды на интегрируемость и диф-ференцируемость, а также применять теоремы о дифференцируемости и интегрируемости рядов для нахождения их суммы. Для окончательного закрепления на дом будут заданы аналогичные примеры.

Домашнее задание: Практическое занятие №14 из [9].

Ниже приведены решенные номера домашнего задания:

Пример №36 (№95 из [10]).

Можно ли к ряду

Образование, педагогика, воспитание:

Диагностическое исследования уровня коммуникативной полноценности речи учащихся 4-х классов
Речь у детей младшего школьного возраста обычно развивается параллельно с совершенствованием мышления, особенно словесно-логического, поэтому, когда проводится психодиагностика развития мышления, она частично затрагивает речь, и наоборот: когда изучается речь ребенка, то в получаемых показателях не ...

Формирование репродуктивных и рецептивных грамматических навыков
Разный характер действий, лежащих в основе рецептивной и репродуктивной деятельности ставит на первое место задачу развития продуктивных и рецептивных грамматических навыков и умений, выработку грамматических механизмов речи. Поэтому упражнения занимают центральное место при обучении иностранному я ...

Методы, способствующие развитию познавательной активности учащихся на уроках биологии
Степень активности учащихся является реакцией, методы, и приемы работы преподавателя являются показателем его педагогического мастерства. Активными методами обучения следует называть те, которые максимально повышают уровень познавательной активности школьников, побуждают их к старательному учению. ...