Электронное пособие по теме “Функциональные последовательности и ряды"
Исследуем ряд 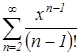 на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
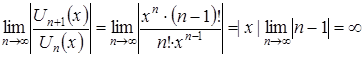 ,
,
так как ![]() , то условие абсолютной сходимости ряда не выполняется при
, то условие абсолютной сходимости ряда не выполняется при ![]() R. Следовательно, ряд
R. Следовательно, ряд 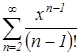 расходится.
расходится.
Значит, к заданному функциональному ряду нельзя применить теорему о почленном дифференцировании.
Ответ: Теорему о почленном дифференцировании к ряду ![]() применить нельзя.
применить нельзя.
Пример №39 (№115 из [10]).
Показать, что ряд 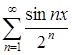 допускает почленное интегрирование на отрезке
допускает почленное интегрирование на отрезке ![]() , написать полученный при этом ряд.
, написать полученный при этом ряд.
Решение
Функциональный ряд 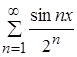 можно интегрировать почленно на отрезке
можно интегрировать почленно на отрезке ![]() , если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
, если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
Элементы функционального ряда 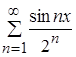 являются непрерывными функциями для
являются непрерывными функциями для ![]() R, значит, и на отрезке
R, значит, и на отрезке ![]() .
.
Кроме того, по признаку Вейерштрасса заданный функциональный ряд равномерно и абсолютно сходится на R, а, значит, и на отрезке ![]() . Действительно, так как:
. Действительно, так как:
а) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 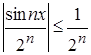 при
при ![]() R;
R;
в) 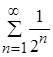 - числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии с
- числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии с 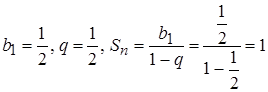 ).
).
Значит, теорему о почленном интегрировании можно применить к функциональному ряду 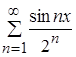 на отрезке
на отрезке ![]() .
.
Ряд полученный при почленном интегрировании заданного ряда, примет вид 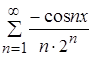 на отрезке
на отрезке ![]() .
.
Ответ: 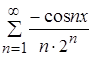 при
при ![]() .
.
Пример №40 (№119 из [10])
Определить область существования функции 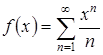 и исследовать ее на дифференцируемость во внутренних точках существования.
и исследовать ее на дифференцируемость во внутренних точках существования.
Решение
Определим область сходимости ряда 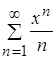 . По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
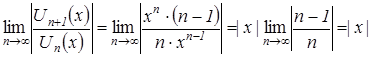 ,
,
если ![]() , т.е.
, т.е. ![]() , то заданный функциональный ряд сходится абсолютно.
, то заданный функциональный ряд сходится абсолютно.
При ![]() ряд примет вид
ряд примет вид 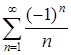 . Полученный ряд сходится условно, так как удовлетворяет условиям признака Лейбница (признак сходимости числовых знакочередующихся рядов), т.е.
. Полученный ряд сходится условно, так как удовлетворяет условиям признака Лейбница (признак сходимости числовых знакочередующихся рядов), т.е. ![]() и
и ![]() .
.
Образование, педагогика, воспитание:
Познавательное развитие детей в ДОУ
Накопленные к шести годам сведения о большом мире является серьезной базой для дальнейшего развития познавательной сферы ребенка. Эта база данных о большом мире требует от него определенных умений и упорядочивания накопленных и поступающих сведений. Процесс знаний направлен на: - содержательное упо ...
Роль семьи в полоролевой социализации дошкольников
До сих пор ученые полемизируют: какое понятие шире - полоролевое или половое воспитание. Одни считают полоролевое воспитание составной частью полового, другие убеждены в том, что оно (полоролевое) - более широкая область воспитания по сравнению с сексуальным. Но те и другие едины во мнении: психосе ...
Психологическая характеристика старшеклассника
Особенность этого возраста в том, что "начинается" он с изменения социальной ситуации развития. Этот возраст исследовали многие видные психологи. Впервые описал психологические особенности подросткового возраста С.Холл, который указал на противоречивость поведения. Как уже отмечалось, что ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

