Электронное пособие по теме “Функциональные последовательности и ряды"

применить теорему о дифференцировании функциональных рядов?

Решение

Функциональный ряд можно почленно продифференцировать, если члены ряда и производные его членов непрерывны, а сам ряд и ряд, составленный из производных членов его ряда, сходятся равномерно на данном промежутке.

Рассмотрим заданный функциональный ряд :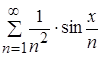

a) члены ряда являются непрерывными функциями для R, N;

б) так как 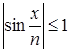при R, N, то справедливо неравенство 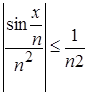при R, N;

в) но 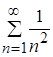- числовой положительный сходящийся ряд (ряд Дирихле с );

г) значит, функциональный ряд 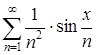сходится равномерно и абсолютно при R по признаку Вейерштрасса.

Составим ряд из производных членов заданного функционального ряда

.

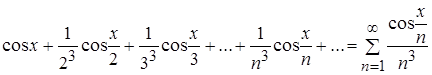Исследуем полученный функциональный ряд:

a) члены ряда являются непрерывными функциями для R, N;

б) так как 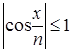при R, N, то справедливо неравенство 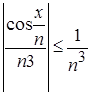при R, N;

в) но 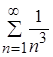- числовой положительный сходящийся ряд (ряд Дирихле с );

г) значит, функциональный ряд 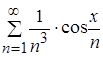сходится равномерно и абсолютно при R по признаку Вейерштрасса.

Следовательно, заданный функциональный ряд 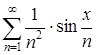можно почленно дифференцировать.

Ответ: Теорему о почленном дифференцировании применить можно.

Пример №36 (№96 из [10]).

Можно ли к ряду 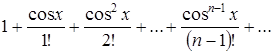применить теорему об интегрировании функциональных рядов в любом конечном промежутке ?

Решение

Функциональный ряд 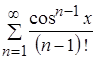можно почленно интегрировать на отрезке , если на указанном промежутке его члены непрерывны, и ряд равномерно сходится.

Элементы функционального ряда 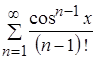являются непрерывными функциями для R.

Кроме того, по признаку Вейерштрасса заданный функциональный ряд равномерно и абсолютно сходится на R, а, значит, и на отрезке .

Образование, педагогика, воспитание:

Игры с использованием предметных и сюжетных картинок
Уже в конце первого года ребенок тянется к красочной картинке, радуясь изображению. Малыш не сразу отличает реальный предмет от его изображения на картинке. Он относится к рисунку как к игрушке, к вещи, пытаясь взять нарисованный мячик, укусить яблоко. С помощью взрослого малыш постепенно устанавли ...

Физическое воспитание – одна из важных сторон гармоничного развития личности ребенка дошкольного возраста
В качестве одного из видов воспитания физическое воспитание представляет собой воспитательно-образовательный процесс, характеризующийся всеми присущими педагогическому процессу общими признаками (ведущая роль педагога специалиста, направленность деятельности воспитателя и воспитуемых на реализацию ...

Учебник математики
Назначение учебника математики Учебник математики – книга, излагающая основы научных знаний по математике в соответствии с целями обучения, определёнными программой и требованиями дидактики. Содержание и построение учебника определяется задачами преподавателя математики и спецификой предмета и пото ...