Электронное пособие по теме “Функциональные последовательности и ряды"

При ряд примет вид -расходящийся гармонический ряд.

Значит, - область сходимости заданного ряда, причем элементы ряда являются непрерывными функциями на всей области сходимости.

Найдем производную общего члена ряда: 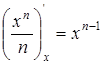. Ряд из производных сходится при , как сумма убывающей геометрической прогрессии. Причем, элементы ряда также являются непрерывными при .

Значит, ряд 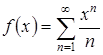можно продифференцировать во всех внутренних точках интервала .

Ответ: Заданный функциональный ряд можно почленно дифференцировать на интервале .

§9. Результаты пробация

В осеннем семестре 2003-2004 учебного года были апробированы лекционные и практические занятия, а также тест по теме "Функциональные последовательности и ряды" на втором курсе факультета математики и информатики СГПИ.

Материалы фондовых лекций по вышеуказанной теме были продемонстрированы студентам в электронном виде. Для проведения лекций использовался компьютер с TV-кодером и телевизор с большой диагональю экрана (71см). Текст лекции с жесткомагнитного диска подавался на экран и озвучивался лектором. Применяемая методика проведения лекционных занятий с использованием новейших информационных технологий позволила увеличить скорость подачи информации в 1,5 раза и улучшила качество содержания конспектов студентов.

При хорошей подготовке и исключении “накладок" использование в лекции даже простых технических средств предъявления информации может существенно повысить её привлекательность для студентов, дидактическую эффективность, а также снизить нагрузку на голосовой аппарат преподавателя.

Об эффективности разработанной методики проведения практических занятий можно судить по результатам самостоятельных работ, проводимых по каждому практическому занятию.

Образование, педагогика, воспитание:

Оздоравливающие пальчиковые игры
Многие уже слышали об иглорефлексотерапии. Через активные точки на коже человека не только иглами, но и лазерным лучом, и электропунктурой восстанавливают работу энергетических каналов. Каждый такой канал регулирует деятельность определенного органа, а то и системы органов тела. Пользуйтесь целебны ...

Типологический отбор исследуемых
Допустим, необходимо изучить эффективность нового метода развития силы. Для эксперимента потребуется сформировать две группы исследуемых, предположим, по 10 человек. Однако судить об эффективности нового метода позволительно будет только в том случае, если удастся уравнять исходные уровни развития ...

Справочная и научно-популярная литература и методика их использования. Учебное оборудование по математике и методика использования его в учебной работе
Обучение пользованию справочниками по математике, справочными таблицами и другой справочной литературой должно найти своё место при изучении математики в средней школе. Справочники необходимы по той причине, что для запоминания выбирается первостепенное, необходимое для изучения дальнейшего курса, ...