Электронное пособие по теме “Функциональные последовательности и ряды"

Пример№30 (№ 343 из [7], с комментариями преподавателя).

Можно ли к ряду

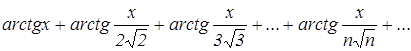
применить теорему о почленном дифференцировании рядов?

Решение

Известно, что почленное дифференцирование функционального ряда возможно, если члены ряда и их производные непрерывны, а сам ряд и ряд, составленный из производных, сходятся в данном промежутке равномерно.

Сравним исследуемый функциональный ряд 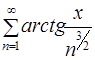с функциональным рядом 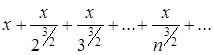при любом фиксированном .

Предварительно заметим, что функциональный ряд 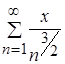равномерно и абсолютно сходится при R в соответствии с признаком Вейерштрасса.

Действительно, при R справедливо неравенство 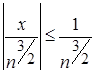. А положительный числовой ряд 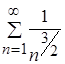является сходящимся. Это ряд Дирихле (или обобщенный гармонический ряд с ).

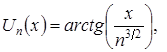
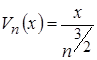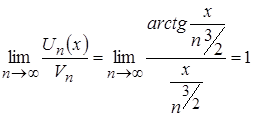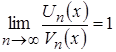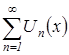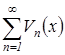Обозначим общие элементы сравниваемых рядов Так как при и - бесконечно малые величины, то . В соответствии со вторым признаком сравнения рядов, так как существует конечный, отличный от нуля предел , то оба ряда и одновременно сходятся или одновременно расходятся.

Но ряд 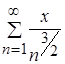абсолютно и равномерно сходится для R, значит, функциональный ряд 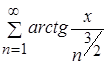сходится равномерно и абсолютно при . Кроме того, члены ряда - непрерывные функции при R.

Найдем производную общего элемента функционального ряда

: .

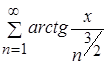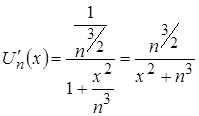Ряд, составленный из производных членов исходного функционального ряда, имеет вид:

.

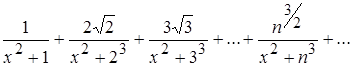Все элементы записанного ряда представляют собой непрерывные функции на R.

Докажем, что ряд 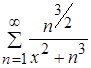равномерно и абсолютно сходится на R.

Очевидно, что для R выполняется следующие неравенства: 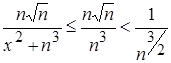. Но числовой положительный ряд 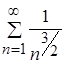сходится, так как является обобщенным гармоническим рядом (ряд Дирихле) с . В соответствии с признаком Вейерштрасса, будет равномерно и аболютно сходиться ряд 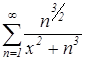при R. А это ряд, составленный из производных чледов исследуемого функционального ряда.

Образование, педагогика, воспитание:

Теоретические основы преподавания живописи пейзажа акварелью
Для преподавания живописи пейзажа акварелью на уроках изобразительного искусства необходимо для начала ознакомить учащихся с различными видами пейзажей, картинами художников и разными акварельными техниками. Необходимо начать с выполнения простых упражнений, небольших этюдов пейзажа, а также деталь ...

Осознание педагогической задачи, анализ исходных данных и постановка педагогического диагноза
В творческом процессе педагога одновременно или последовательно должны осмысливаться разные педагогические задачи. Прежде всего это должна быть общая педагогическая задача всей деятельности учителя, которая выступает как его общая концепция. Затем должна осмысливаться этапная педагогическая задача, ...

Повышение уровня двигательной активности и дозировка физической нагрузки на физкультурных занятиях
В последние годы ведущими направлениями в исследованиях по физической культуре стали изучение эффективности двигательной активности детей, совершенствование количественных и качественных показателей развития движений. Исследования профессора И.А.Аршавского говорят о том, что у ребенка восстановлени ...