Электронное пособие по теме “Функциональные последовательности и ряды"

Остаток исследуемого функционального ряда будет не больше остатка числового положительного ряда, т.е. .

Найдем теперь, при каком значении будет выполняться неравенство .

Для этого необходимо решить неравенство , , .

Ответ: При .

В конце занятия подводятся итоги, выставляются оценки, оговаривается домашнее задание.

Преподаватель: Итак, подведем итог: на сегодняшнем занятии мы с вами научились исследовать функциональный ряд на равномерную сходимость с помощью определения равномерной сходимости и признака Вейерштрасса. Для окончательного закрепления на дом будут заданы аналогичные примеры.

Домашнее задание: практическое занятие №13 из [9].

Ниже приведены решенные номера домашнего задания.

Пример №23 (№54 из [10]).

Показать, что ряд 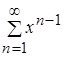сходится неравномерно в интервале .

Решение.

В указанном интервале ряд сходится как бесконечно убывающая геометрическая прогрессия. Имеем т.е. .

Но 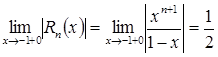, 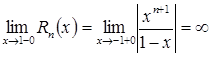. Следовательно, приняв , невозможно добиться выполнения неравенства при . Итак, ряд 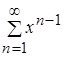сходится неравномерно на интервале .

Ответ: Доказана неравномерная сходимость на интервале .

Пример №24 (№63 из [10]).

Исследовать на равномерную сходимость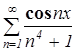 на промежутке .

Решение

Так как N, R, то в качестве мажорантного ряда выберем 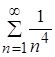- числовой положительный ряд. Он сходится, так как это ряд Дирихле с . Тогда, по теореме Вейерштрасса равномерной и абсолютной сходимости функциональных рядов, ряд 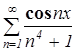сходится равномерно и абсолютно на промежутке , так как выполняется неравенство 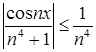при .

Ответ: Заданный ряд сходится абсолютно и равномерно на интервале .

Пример №25 (№ 66 из [10]).

Исследовать на равномерную сходимость 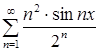на промежутке .

Образование, педагогика, воспитание:

Сущность педагоических инноваций
Педагогические инновации (другими словами нововведения) определяются в педагогической науке с нескольких точек зрения. Во-первых, под педагогической инновацией понимается целенаправленное изменение, вносящее в образовательную среду стабильные элементы (определённые новшества), которые улучшают хара ...

Задачи внеклассной работы по физическому воспитанию
Одним из видов внеклассной работы в школе является массовая физкультурная и спортивная работа. Задачи внеклассной работы: -содействовать школе в выполнении стоящих перед ней учебно-воспитательных задач; -содействовать укреплению здоровья, закаливанию организма, разностороннему физическому развитию ...

Программа совершенствования педагогической деятельности
Исследования ученых и анализ практики показывает, что значительная часть педагогов учреждений дополнительного образования детей часто действуют стереотипно в силу сложившихся традиций. В настоящее время востребованы переоценка педагогом своего педагогического труда, выход за пределы традиционной ис ...