Электронное пособие по теме “Функциональные последовательности и ряды"

Вопрос 4: Сформулировать достаточный признак равномерной сходимости функционального ряда - признак Вейерштрасса.

Ответ: Теорема. Пусть даны два ряда: функциональный , элементами которого являются функции , определенные на множестве, и числовой положительный сходящийся ряд . Тогда, если для всех выполняется неравенство , то функциональный ряд равномерно и абсолютно сходится на множестве .

Преподаватель: А теперь рассмотрим задание на исследование равномерной сходимости функционального ряда.

Пример №16 (№349 из [7], c комментариями преподавателя).

Показать, что ряд

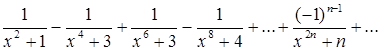
сходится равномерно при всех действительных значениях .

Решение

Данный ряд при любом значении сходится по признаку Лейбница, поэтому его остаток оценивается с помощью неравенства , т.е.

.

Так как неравенства и равносильны, то, взяв , где - какое-нибудь целое положительное число, которое удовлетворяет условию , приходим к неравенству . Итак, данный ряд сходится рав-номерно в промежутке при всех .

Ответ: Доказана равномерная сходимость для R.

Пример №17 (№51 из [10], студент у доски с помощью преподавателя).

Исследовать на равномерную сходимость ряд

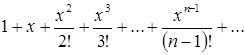
на любом конечном интервале.

Решение

Докажем, что каково бы ни было число , данный ряд сходится равномерно и абсолютно в круге радиусом , т.е. .

Заданный ряд сходится при любом значении , в частности, при , получаем числовой ряд: .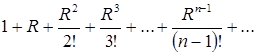

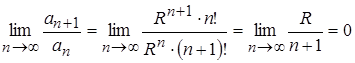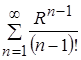Исследуем его на абсолютную сходимость, применив признак Даламбера . Так как , то ряд сходится, причем абсолютно.

Возьмем этот ряд в качестве мажорантного, по признаку Вейерштрасса равномерной сходимости функционального ряда 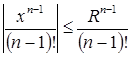при .

Образование, педагогика, воспитание:

Формы занятий и контроль знаний на элективных курсах по математике
Введение профильного обучения, а особенно элективных курсов, в программу старшей школы, несомненно, потребует разнообразия форм и методов обучения, так как профильное обучение – это не только дифференцирование содержания образования, но, как правило, и по-другому построенный учебный процесс. При вы ...

Технология педагогических мастерских
Существующая система образования в значительной степени построена на передаче знаний от учителя к ученику, на пассивной позиции обучающегося, что не позволяет личности самой строить свое знание, активно и творчески пользоваться им в жизни как свои приобретением. Этот подход к образованию не раскрыв ...

Специфика обучения и воспитания детей с нарушениями слуха
Глухой и слабослышащий ребенок, как и слышащий, при рождении — существо, открытое миру, которому необходимо воспитание как помощь в жизни. В соответствии со своей биологической сущностью он способен к обучению и может в процессе социализации получить воспитание и образование, которые станут предпос ...