Электронное пособие по теме “Функциональные последовательности и ряды"

Отсюда, - интервал сходимости заданного функционального ряда.

Определим сходимость ряда в точках и .

Если , то ряд примет вид - числовой знакочередующийся ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. . Следовательно, заданный функциональный ряд расходится в точке .

Если , то ряд примет вид - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. . Следовательно, исследуемый функциональный ряд расходится в точке .

Значит, - область абсолютной сходимости заданного функционального ряда. Ответ: .

Пример №14 (№15 из [10]).

Найти сумму ряда

.

Решение

По признаку Даламбера абсолютной сходимости функционального ряда имеем:

.

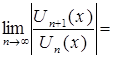
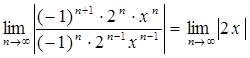Если , т.е. 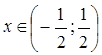, то заданный функциональный ряд сходится абсолютно на указанном интервале.

Если , т.е. 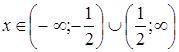, исследуемый функциональный ряд расходится.

При функциональный ряд примет вид 1+1+1+… - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. . Следовательно, в точке исследуемый функциональный ряд расходится.

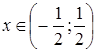При функциональный ряд примет вид 1-1+1-1+… - числовой знакочередующийся ряд. Он расходится, так как ни одно из двух условий признака Лейбница не выполняется: а) ; б) . Значит, функциональный ряд в точке расходится. Значит, - область абсолютной сходимости заданного функционального ряда.

На области своей сходимости исследуемый ряд представляет собой сумму убывающей геометрической прогрессии. Сумму этой прогрессии найдем по формулам:

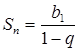, где .

Тогда, при .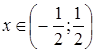

Ответ: при .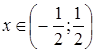

Образование, педагогика, воспитание:

Национальные традиции и культура как область воспитательных воздействий в ДОУ
В современных условиях осознания духовных основ развития общества актуальной является проблема глубокого и научно-обоснованного учета особенностей региональной культуры в работе с детьми. Необходимость внедрения регионального компонента предусмотрена Законом РФ. В содержании отдельных разделов дошк ...

Анализ программ и технологий
Основной целью воспитания ребенка является всестороннее и гармоничное развитие его личности. Физическое воспитание - неотъемлемая часть этого процесса. В обществе ведется активная пропаганда здорового образа жизни: отказ от вредных привычек, активный отдых и, конечно, занятия физкультурой, которой ...

Экологическая составляющая химического образования
Современная экология – обширный междисциплинарный научный комплекс. Наряду с общей экологией, исследующей отношения организмов и условий среды на уровне особей, популяций, биоценозов и экосистем, этот комплекс включает прикладную экологию и социальную экологию. Столь широкий круг проблем экологии п ...