Электронное пособие по теме “Функциональные последовательности и ряды"

Таким образом, областью абсолютной сходимости исследуемого функционального ряда является интервал .

Ответ: .

Пример №12 (№38 из [10]).

Найти область сходимости ряда

Решение. По признаку Даламбера абсолютной сходимости функционального ря-да имеем:

.

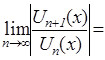
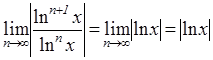Если, т.е. , или , то функциональный ряд сходится абсолютно на интервале .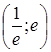

Если , т.е. 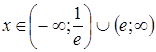, то ряд расходится.

При функциональный ряд становится числовым знакочередующимся рядом . Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а) ; б) .

Значит, функциональный ряд расходится в точке .

При функциональный ряд становится положительным числовым рядом . Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда .

Значит, функциональный ряд расходится в точке .

Таким образом, область абсолютной сходимости исследуемого ряда есть интервал .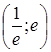

Ответ: .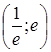

Пример №13 (№5 из [10]).

Найти область сходимости функционального ряда:

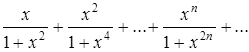
Решение

По признаку Даламбера абсолютной сходимости функционального ря-да имеем:

.

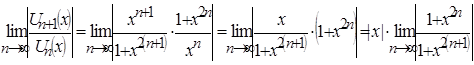Если , то

.

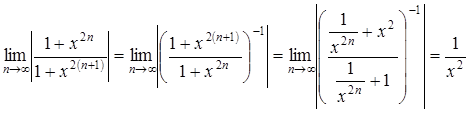Тогда .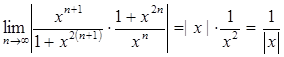

Если , т.е. , то заданный ряд сходится абсолютно.

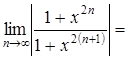Если , то 1.

Тогда, 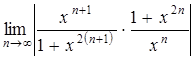=. Если , т.е. , то заданный функциональный ряд сходится абсолютно.

Образование, педагогика, воспитание:

Игровые технологии преподавания происхождения сущности государства и права в современной школе
Игра – это определенная целостная реальность, обязательно как-то соотносящаяся с существующим миром («кусок» жизни). В этой реальности действуют и общаются люди. Соответственно, в процессе игры играющие получают опыт. Составляющими опыта могут быть и знания, и эмоциональные впечатления, и навыки, и ...

Цели и формы музыкального образования в европейской истории образования
Музыкальное образование — процесс и результат усвоения систематизированных знаний, умений и навыков, необходимых для музыкальной деятельности. Под музыкальным образованием понимают также систему организации музыкального обучения в музыкальных учебных заведениях. Важную роль может играть и самообраз ...

Анализ профессионального образа педагога на примере средней общеобразовательной школы
Учитывая, что не каждый педагог целенаправленно задумывается о формировании собственного профессионального имиджа, следует при исследовании акцентировать внимание педагогов на определенные высказывания, касающихся восприятия учащимися некоторых характеристик личности педагога. Суждения, представлен ...