Электронное пособие по теме “Функциональные последовательности и ряды"

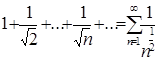При получим числовой положительный ряд . Это ряд Дирихле с . Известно, что если , то ряд 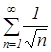расходится. Значит, функциональный ряд в точке расходится.

При получим числовой знакочередующийся ряд вида 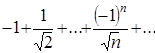. Он сходится, так как удовлетворяет условиям признака Лейбница сходимости знакочередующихся числовых рядов, т.е. и : .

Ряд, составленный из абсолютных величин элементов ряда 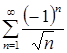, имеет вид и является расходящимся.

Значит, функциональный ряд сходится условно в точке x=1.

Итак, область сходимости исследуемого функционального ряда . Абсолютно ряд сходится на интервале .

Ответ: .

Преподаватель: Последний вид заданий, который мы с вами сегодня рассмотрим, - на нахождение суммы функционального ряда.

Пример №8 (№14 из, с комментариями преподавателя).

Найти сумму ряда:

.

Решение

По признаку Даламбера абсолютной сходимости функционального ряда можем записать:

.

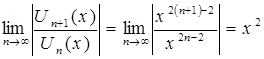Если , т.е. то функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то исследуемый функциональный ряд расходится на указанных промежутках.

При функциональный ряд становится числовым положительным расходящимся рядом , так как не выполняется необходимое условие сходимости числового ряда, т.е. .

Значит, область абсолютной сходимости функционального ряда есть интервал .

Найдем сумму заданного функционального ряда на его области сходимости.

Если , то исследуемый ряд представляет собой сумму убывающей геометрической прогрессии с . Сумму ряда будем определять по формуле:

.

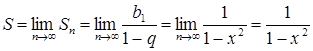При сумма ряда .

Образование, педагогика, воспитание:

Использование познавательных книг математического содержания и рабочих тетрадей в логико-математическом развитии дошкольников
На протяжении XX в. активно разрабатывались вопросы использования книг с математическим содержанием и рабочих тетрадей с целью обогащения математических представлений дошкольников (Ф. Н. Блехер, 3. А. Михайлова, Л. Г. Петерсон, Е. Я. Фортунатова, Л. К. Шлегер и др.). Условно можно выделить нескольк ...

Проектирование и изготовление ветряка
Требования к ветряку. Ветродвигатель должен работать при слабом порыве ветра. Ветряк должен работать при постоянных переменах направления ветра. Лопасти ветродвигателя должны быть изготовлены из тонкого, легкого, упругого материала. Лопасти должны иметь дугообразную форму. Ветродвигатель должен быт ...

Характеристика теоретических подходов к функциям семьи в современном социуме
Семья – необходимая составляющая социальной структуры цивилизованного общества, исторически изменяющееся явление, функционирующая как институт воспроизводства человека и его воспитания. Семья является тем социально-культурным образованием, где индивид получает первый опыт организации жизнедеятельно ...