Электронное пособие по теме “Функциональные последовательности и ряды"

Пример№15 (№ 17 из [10]).

Найти сумму ряда

.

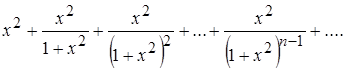Решение

По признаку Даламбера абсолютной сходимости функционального ря-да имеем:

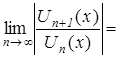
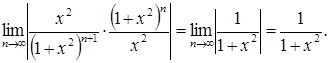
Если , т.е. заданный функциональный ряд сходится абсолютно.

На области своей области сходимости ряд представляет собой сумму убывающей геометрической прогрессии. Сумму этой прогрессии найдем по формулам:

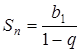, где .

Тогда, 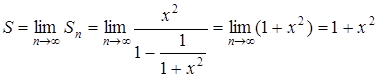при R/0.

Ответ: при R/0.

Практическое занятие №2

Тема: "Равномерно сходящиеся функциональные последовательности и ряды"

Тип занятия: практикум решения задач.

Форма занятия: комбинированная между коллективной и фронтальной.

Средства обучения на занятии: сборник задач, методические рекомендации к практическим занятиям, телевизор, подключенный к компьютеру, графопроектор, доска, мел.

Цель: закрепление знаний полученных на лекции, применение их на практике.

Методы: словесные, наглядные, по дидактической цели - познавательные, по характеру познавательной деятельности - проблемные.

Ход занятия:

1. Организационная часть: Студентам сообщается тема практического занятия, его цель, проверка присутствующих (3 минуты).

2. Основная часть: Проверка домашнего задания с помощью теста (20 минут). Фронтальный опрос по изученной теме (12 минут). Ознакомление с новым материалом, первичное закрепление и осмысление (50 минут). Затем, подведение итогов и постановка домашнего задания (5 минут).

Конспект занятия

Преподаватель: Тема занятия: "Равномерно сходящиеся функциональные последовательности и ряды". Цель - приобрести навыки решения задач по вышеуказанной теме. Но прежде, проведем самостоятельную работу, которая позволит определить, насколько успешно вы справились с домашним заданием.

Если есть возможность провести занятие в компьютерном классе, то самостоятельная работа по домашнему заданию проводится с помощью теста. Для этого преподавателю необходимо до начала занятия установить программу на компьютеры. Чтобы студенты могли приступить к тестированию, преподавателю также нужно ввести пароль. Студенту необходимо внести свои данные (Ф.И.О., курс, группе). Только тогда он сможет пройти тестирование, а результат будет внесен в журнал. В тесте предлагается три вида заданий: а) исследовать сходимость функционального ряда в точке; б) определить область сходимости функционального ряда; в) найти сумму функционального ряда. Во время прохождения теста программой случайным образом выбирается по одному примеру из каждого вида заданий (всего выбирается 3 примера) и предлагается студенту для решения. Все примеры были решены на предыдущей практике или являлись домашним заданием. На каждое задание, чтобы решить его и выбрать правильный ответ из предложенных четырех, предоставляется 5 минут. Студент не может прервать тестирование, пока не решит все три задания или пока не закончится время тестирования. По окончании тестирования выдается результат в виде оценки, который автоматически вносится в журнал. В приложении приводятся тестовые задания с указанием правильных ответов.

Образование, педагогика, воспитание:

Методические аспекты изучения персоналий в школьном курсе истории
Главный элемент содержания исторического образования – знания. Они включают в себя сведения, познания в области истории, концентрируя социальный опыт человечества. Знания создают научную картину развития общества, дают представление об исторической действительности и предполагают постижение её чело ...

Организация учебного процесса в коммуникативном направлении отечественной методики
В теоретических основах коммуникативного метода, разработанного Е.И. Пассовым, даются ссылки на теорию деятельности А.Н. Леонтьева, теорию речевого общения А.А. Леонтьева, теорию речевой деятельности И.А. Зимней, работы Л.С. Выготского, С.Л. Рубинштейна. Коммуникативный метод представляет условия и ...

Игры, формирующие правильное звукопроизношение
Общение ребенка со взрослыми и сверстниками наиболее успешно осуществляется тогда, когда говорящий внятно и чисто произносит слова. Нечеткое или неправильное произношение слов может быть причиной их непонимания. Неправильное произношение отдельных групп звуков в младшем дошкольном возрасте вполне з ...