Электронное пособие по теме “Функциональные последовательности и ряды"
исследовать его сходимость в точках ![]() и
и ![]() .
.
Решение
В точке ![]() получаем числовой положительный ряд
получаем числовой положительный ряд
![]() .
.
Исследуем полученный ряд на сходимость, применив признак Далам-бера сходимости положительного числового ряда:
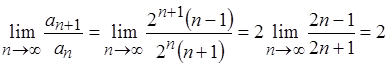 ,
,
так как ![]() , то числовой положительный ряд расходится. А значит, заданный функциональный ряд расходится в точке
, то числовой положительный ряд расходится. А значит, заданный функциональный ряд расходится в точке ![]() .
.
В точке ![]() получаем числовой положительный ряд:
получаем числовой положительный ряд:
![]() .
.
Исследуем полученный ряд на сходимость, применив признак Даламбера сходимости положительного числового ряда:
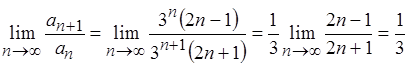 ,
,
так как ![]() , то числовой положительный ряд
, то числовой положительный ряд 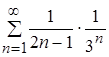 сходится. Следовательно, функциональный ряд
сходится. Следовательно, функциональный ряд 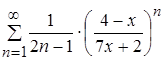 сходится, причем абсолютно, в точке
сходится, причем абсолютно, в точке ![]() .
.
Ответ: Функциональный ряд сходится абсолютно при ![]() и расходится при
и расходится при ![]() . Пример №2 (№345 из, студент решает у доски самостоятельно). Дан функциональный ряд:
. Пример №2 (№345 из, студент решает у доски самостоятельно). Дан функциональный ряд:
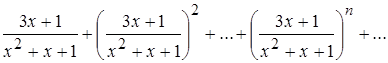 .
.
Исследовать его сходимость в точках ![]() ,
, ![]() и
и ![]() .
.
Решение
При ![]() ряд примет вид
ряд примет вид 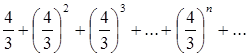 - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е.
- числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. ![]() .
.
При ![]() ряд примет вид
ряд примет вид ![]() - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е.
- числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. ![]() .
.
При ![]() ряд примет вид
ряд примет вид 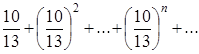 . числовой положительный ряд. По признаку Даламбера сходимости числового положительного ряда имеем:
. числовой положительный ряд. По признаку Даламбера сходимости числового положительного ряда имеем: 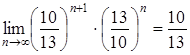 , т.е. ряд сходится. Значит, исходный функциональный ряд сходится в точке
, т.е. ряд сходится. Значит, исходный функциональный ряд сходится в точке ![]() абсолютно.
абсолютно.
Ответ: Заданный функциональный ряд сходится абсолютно в точке ![]() и расходится в точках
и расходится в точках ![]() и
и ![]() .
.
Пример №3 (№1 из [10], с комментариями преподавателя).
Найти область сходимости функционального ряда:
![]() .
.
Решение
I способ.
Образование, педагогика, воспитание:
Проверка результатов эксперимента
Особенно важное значение имеет проверка полученных в ходе педагогического эксперимента результатов на практике, в повседневной работе. Дело в том, что экспериментатор независимо от желания всегда находится в лучших условиях для проведения учебно-воспитательной работы, чем обычный преподаватель. Выс ...
Теоретические основы формирования экологической компетентности будущего инженера
В России уровень смертности населения трудоспособных возрастов от несчастных случаев, отравлений и травм, в том числе производственных, в настоящее время соответствует аналогичным показателям столетней давности, почти в 2,5 раза превышает показатели, сложившиеся в развитых странах, и в 1,5 раза ...
Урочные формы внеклассной работы
Прогулки, экскурсии и походы имеют большое образовательное и воспитательное значение, поскольку дети знакомятся с природой, родным краем и его достопримечательностями. Эти мероприятия содействуют совершенствованию навыков в ходьбе, беге и играх, закаляют организм и укрепляют здоровье детей, способс ...
Навигация по сайту
- Активизация мышления
- Системы образования в разных странах мира
- Социальная адаптация ребенка
- Социальная работа в школе
- Физическое воспитание дошкольников
- Средства обучения математике
- Другое о педагогике

