Критерий Коши равномерной сходимости функционального ряда

Теорема 2. Для того чтобы функциональный ряд равномерно сходился на множестве X, необходимо и достаточно, чтобы 0, N, , , N и выполнялось неравенство:

.

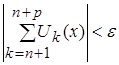Доказательство

1) Составим разность частичных сумм функционального ряда :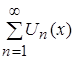

.

2) Если будут выполняться неравенства: , то это означает, что последовательность частичных сумм функционального ряда 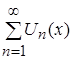равномерно сходится на множестве Х. А по определению равномерной сходимости функционального ряда, исследуемый функциональный ряд будет сходиться на множестве Х.

Достаточный признак равномерной и абсолютной сходимости функционального ряда (признак Вейерштрасса)

Теорема 3. Пусть даны два ряда: функциональный 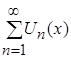, элементами которого являются функции , определенные на множестве Х, и числовой положительный сходящийся ряд 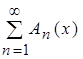. Тогда, если для всех выполняется неравенство , то функциональный ряд 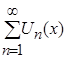равномерно и абсолютно сходится на множестве Х.

Доказательство:

Пусть выполняются все условия теоремы.

Так как по условию теоремы числовой ряд сходится, то в соответствии со свойством числового ряда, его остаток должен стремится к нулю, т.е. или .

Так как это положительный числовой ряд, то неравенство примет вид:

По условию теоремы выполняется неравенство: . Поэтому, при выполняется и такое неравенство: .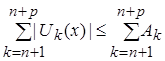

Если , то неравенство примет вид: 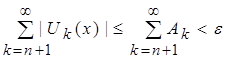(с учетом пункта 2). По свойству транзитивности 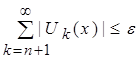- это остаток положительного функционального ряда, стремящегося к нулю при . Значит, функциональный ряд 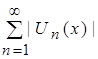будет сходиться по свойству рядов. Известно, что если ряд абсолютно сходится, то он просто сходится. Значит, функциональный ряд 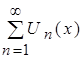сходится.

Образование, педагогика, воспитание:

Влияние игры на формирование элементов учебной деятельности и интеллектуальной подготовки детей
Подготовка к школе органично входит в жизнь ребенка, если взрослые учитывают психологическую специфику дошкольного возраста, не забывая о ведущей роли игры в этом периоде развития личности. Академик А.В.Запорожец писал, что оптимальные педагогические условия для реализации потенциальных возможносте ...

Трудности социальной адаптации одаренного ребенка
Многочисленные исследования показывают преимущества одаренных детей в когнитивной сфере, они свидетельствуют также о том, что дети с необычайно высоким интеллектуальным коэффициентом сочетают в себе черты социальной привлекательности, физического и психологического здоровья, эффективного лидерства ...

Функции наглядности в учебнике математики. Методы работы с учебником
Не все виды наглядностей, применяемых иллюстраций имеют одинаковое значение для раскрытия изучаемых закономерностей. На процесс решения математической задачи существенное влияние оказывает схема и предметно-аналитическая картинка, в которой отражены количественные отношения искомого и данного. Выде ...