Критерий Коши равномерной сходимости функционального ряда

Докажем равномерность сходимости функционального ряда. Из неравенства 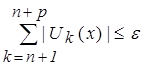и, используя свойства модуля суммы двух действительных чисел () можно переписать это неравенство так:

.

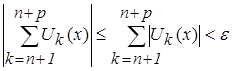По свойству транзитивности: 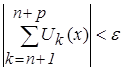- условие равномерности сходимости функционального ряда на множестве Х.

Замечание. Положительный сходящийся числовой ряд, связанный с функциональным рядом, называется мажорантным или мажорирующим.

Пример №3: Доказать, что функциональный ряд абсолютно и равномерно сходится на всей числовой прямой.

Решение

1) Так как , N, R, то в качестве мажорантного ряда выберем при R.

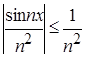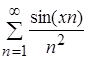2) Cравним общие элементы функционального и числового рядов: , при R. Следовательно, сходится абсолютно и равномерно на R, так как 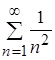- положительный сходящийся ряд (ряд Дирихле с ) [4]. Замечание. Признак Вейерштрасса является лишь достаточным условием равномерной сходимости функционального ряда.

Образование, педагогика, воспитание:

Особенности социальной работы в образовательном учреждении
Проблема развития социальной педагогики в России очень актуальна. Официально профессия "социальный педагог" появилась в нашей стране лишь около десяти лет назад. Социальный педагог - призван объединять усилия семьи, школы, общественности, для оказания помощи ребенку. Социальная педагогика ...

Система физкультурно-оздоровительной работы в ДОУ
Мероприятия Возрастные группы Периодичность Кто проводит Обследование 1. Обследование уровня физического развития, физической подготовленности детей 2. Диспансеризация Все Ср., ст., подгот. 2 раза в год (сентябрь, май) 1 раз в год Ст. медсестра Воспитатель по физической культуре Воспитатели групп С ...

Особенности методики обучения элементам игры в хоккей детей старшего дошкольного возраста
Хоккей для детей дошкольного возраста существенно отличается от игры взрослых. Прежде всего упражнениями и играми с клюшкой и шайбой (мячом) решается задача общей физической подготовки ребенка. Дети получают лишь элементарные представления о хоккее. Поэтому при обучении дошкольников можно внести це ...