Свойства равномерно сходящихся функциональных последовательностей и рядов

.

С учетом записанного равенства, равенство пункта 5 примет вид:

.

Сравним равенства пункта 3 и пункта 7. Правые части равны, значит, равны и левые: .

Теорема доказана [14].

§9. Почленное интегрирование функциональных рядов

Теорема 6. Если последовательность непрерывных на функций сходится равномерно на указанном отрезке к предельной функции , то последовательность определенных интегралов с переменным верхним пределом 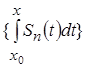будет сходиться равномерно на к определенному интегралу 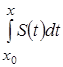, причем будет справедлива следующая формула:

.

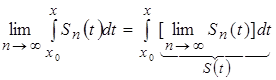1) Так как по условию теоремы последовательность функций равномерно сходится к пределу функции на т.е. , то

функция будет непрерывна на на основании теоремы 5.

2) Известна теорема, что если функция непрерывна на , то она интегрируема на указанном отрезке, т.е. существует определенный интеграл

,

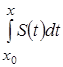3) В силу равномерной сходимости последовательности функции к пределу функции на основании определения равномерной сходимости функциональной последовательности можно записать:

.

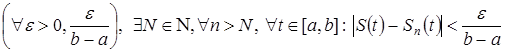4) Рассмотрим разность двух определенных интегралов с переменным верхним пределом под знаком модуля:

=

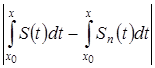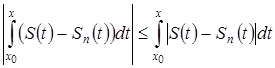
(на основании свойства определенного интеграла).

5) С учетом неравенства пункта 3 можно написать:

.

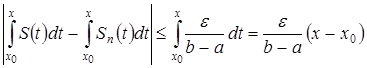6) Если правую часть последнего неравенства заменить на , то получим неравенство:

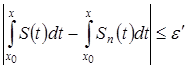, что равносильно выражению

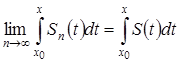, но , поэтому

, .

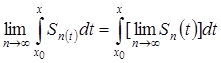Теорема доказана [14].

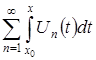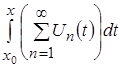Следствие. Пусть функции непрерывны на и функциональный ряд равномерно сходится на указанном отрезке, тогда функциональный ряд вида будет равномерно ходиться на отрезке к или к 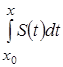, т.е. справедлива

Образование, педагогика, воспитание:

Постановка проблемы в психолого-педагогической литературе
Русский историк Н.И. Караев писал: «История есть, между прочим, и история деятельности людей…». Таким образом, автор нацеливал учащихся средней школы на необходимость глубокой проработки знаний о жизни и деятельности исторических личностей. Поскольку наши исследования были посвящены урокам истории ...

Экспериментальное исследование предметно-развивающей среды как условия обогащения игры-драматизации в старшем дошкольном возрасте
Анализ психолого-педагогической литературы позволил нам предположить, что организация предметно-развивающей среды может рассматриваться как условие обогащения игры-драматизации детей старшего дошкольного возраста, если педагог: организует предметную среду для развития игровых замыслов детей; создае ...

Содержание географических представлений
Взаимодействие человека с природой не может остаться в стороне от познания ребенком окружающего мира. Конкретные примеры использования человеком природных ресурсов, последствия этого воздействия на природу и на здоровье людей могут быть взяты на вооружение дошкольной педагогикой с целью формировани ...