Свойства равномерно сходящихся функциональных последовательностей и рядов

Теорема доказана .

Замечание

1) Полученное утверждение теоремы можно переписать в следующем виде:

или ,

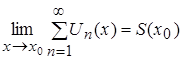так как ,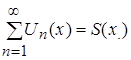

его сумма ,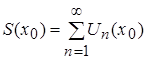

следовательно, .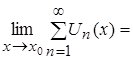

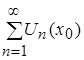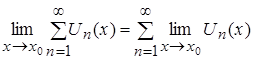2) Так как каждая функция непрерывна в точке , то для любой функции можно написать утверждение: , следовательно, . Таким образом, предел от функционального ряда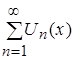равен сумме пределов его элементов.

Известно, что если последовательность частичных сумм функционального ряда равномерно сходится, то этот функциональный ряд тоже равномерно сходится на указанном множестве. Это обстоятельство позволяет переформулировать теорему 4 для функциональных рядов в соответствующую теорему для функциональных последовательностей.

Теорема 5. Если функции , N непрерывны в точке и равномерно сходятся к функции на множестве Х, то и функция непрерывна в точке и выполняется равенство: (предельные переходы по х и по n перестановочны).

Доказательство

Так как функции равномерно сходятся в предельной функции на множестве Х, на основании теоремы 4, то можно записать равенство: .

Функция является непрерывной в точке множества Х на основании теоремы 4. Так как непрерывна в точке , то можно записать следующее утверждение: (определение 1 непрерывности функции в точке).

Используя равенство пункта 1, подставим вместо левую часть утверждения .

Так как по условию теоремы функции непрерывны в точке , то на основании определения 1 непрерывности функции в точке можно записать .

Перейдем к пределу при в последнем равенстве:

.

Так как последовательность функций будет равномерно сходиться к предельной функции , то верно следующее утверждение:

Образование, педагогика, воспитание:

Содержание и экспериментальное обоснование роли семейного физического воспитания в малокомплектной школе
На констатирующем этапе эксперимента мы провели диагностическую работу, которая состояла из двух частей: 1. Выявление потенциала семьи в формировании здорового смысла посредством традиционного семейного физического воспитания. 2. Изучение исходного уровня физической подготовленности школьников. Дан ...

Воспитание нравственных чувств у детей,как средство подготовки детей к обучению в школе
Воспитание нравственных чувств у детей дошкольного возраста тесно связано с формированием у них этических представлений через которые ребенок постигает ценности, без которых невозможна духовная жизнь общества и отдельного человека. Отсутствие таких представлений, незнание того, «что такое хорошо» и ...

Психолого-педагогическая характеристика детей младшего школьного возраста с нарушением интеллекта
Границы младшего школьного возраста, совпадающие с периодом обучения в начальной школе, устанавливаются в настоящее время с 6-7 до 9-10 лет. В этот период происходит дальнейшее физическое и психофизиологическое развитие ребенка, обеспечивающее возможность систематического обучения в школе. Начало о ...