Свойства равномерно сходящихся функциональных последовательностей и рядов

формула: .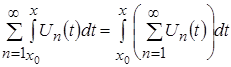

Таким образом, можно сказать, что функциональный ряд можно почленно интегрировать, т.е.

.

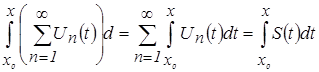Доказательство

1) Так как по условию следствия функциональный ряд 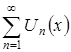равномерно сходится на , то частичная последовательность его функций будет также равномерно сходиться к предельной функции , т.е. .

Причем и непрерывны в каждой точке отрезка на основании только что доказанной теоремы:

.

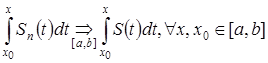3) Но 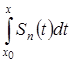представляет собой частичную сумму такого ряда: .

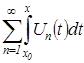4) А 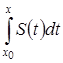является суммой ряда .

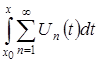На основании доказанной теоремы можно записать:

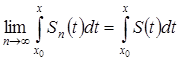
5) Последнее равенство можно переписать следующим образом:

.

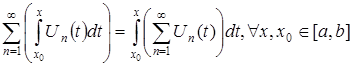Теорема доказана.

Замечание. Условие равномерной сходимости ряда на является лишь достаточным, но не необходимым, поэтому некоторые функциональные ряды, которые равномерно не сходятся, могут быть почленно проинтегрированы.

Образование, педагогика, воспитание:

Влияние процесса саморегуляции на социальную адаптацию одаренного ребенка
Каждый ребенок обладает одному ему присущими свойствами, которые и создают его индивидуальность. Анализ литературных источников по проблеме приводит к выводу о том, что трудности в общении в значительной мере связаны с особенностями личности одаренных. И роль этих особенностей столь велика, что с о ...

Использование познавательных книг математического содержания и рабочих тетрадей в логико-математическом развитии дошкольников
На протяжении XX в. активно разрабатывались вопросы использования книг с математическим содержанием и рабочих тетрадей с целью обогащения математических представлений дошкольников (Ф. Н. Блехер, 3. А. Михайлова, Л. Г. Петерсон, Е. Я. Фортунатова, Л. К. Шлегер и др.). Условно можно выделить нескольк ...

Игры, развивающие внимание и слуховое восприятие
С самого рождения ребенка окружает множество звуков: шум ветра и дождя, шелест листьев, лай собак, сигналы машин, музыка, речь людей и т.д. Но все эти слуховые впечатления воспринимаются малышом неосознанно, сливаясь с другими, боле важными для него сигналами. Ребенок пока еще не умеет управлять св ...