Методические рекомендации для воспитателей по формированию культурно-гигиенических навыков у детей младшего дошкольного возраста

Низкий уровень: на низком уровне остался один ребенок (Оля Т.), другие дети (Артем О.и Ева Б.) повысили свой уровень, то есть из низкого уровня перешли в средний.

Средний уровень: из среднего уровня перешли в высокий уровень трое детей (Маша С., Катя К.и Даниела Б.). Двое детей повысили свой уровень (Маша В.повысила свой уровень с 23 до 28, Олег П.,- с 24 до 30). Двое детей остались на среднем уровне, но у них совершенствовались действия по выполнению отдельных навыков.

Обследование умений уровня сформированности культурно-гигиенических навыков на контрольном этапе эксперимента. Диагностика навыка мытья рук и умывания.

1.Так, закатать рукава полностью могут пятеро детей(50%),

- четверо детей (40%) пытаются закатывать рукава, но справляются только с помощью взрослого;

- один ребенок (10%) не могут закатать рукава.

2. Смочить руки водой сами могут семеро детей (70%);

- трое детей (30%) справляются не полностью;

3. Берут мыло и намыливает до появления пены шестеро детей(60%);

- трое детей (30%) берут мыло, но не могут хорошо намылить руки;

- один ребенок (10%) не может взять мыло и намылить руки.

4. Моют руки самостоятельно шестеро (60%);

- четверо детей (40%)не очень хорошо моют руки.

5. Семеро детей (70%) хорошо смывают мыло с рук;

- двое детей (20%) смывают мыло не достаточно хорошо;

- один ребенок (10%) не может смыть мыло с рук.

6. Семеро детей (70%) сами моют лицо;

- один ребенок (10%) пытается мыть лицо,но делает это не умело;

- двое человек (20%) не умеют мыть лицо.

7. Семеро детей (70%) хорошо вытирает лицо и руки,убираютсалфетку на место;

- трое детей (30%) пытаются вытирать лицо и руки,но делают это не достаточно хорошо.

Отразила навык сформированности мытья рук и умывания в рисунке 7.

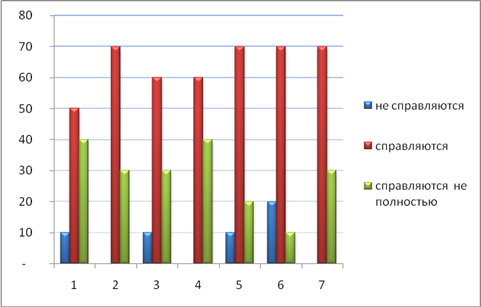
Рисунок 7 - Навык сформированности мытья рук

Условные обозначения: 1- закатать рукава; 2- смочить руки; 3- взять мыло, намылить до появления пены; 4- мыть руки; 5- смыть мыло; 6- мыть лицо; 7-вытереть насухо руки и лицо, повесить полотенце на место.

Диагностика навыка культуры еды.

1.Хорошо держать ложку могут восемь детей (80%);

- двое детей (20%) держат ложку неуверенно, перекладывают из одной руки в другую.

2. Пятеро детей (50%) кусает от кусочка хлеба аккуратно не кроша его;

- четверо детей (40%) не очень аккуратно кушают хлеб;

- один ребенок (10%) не умеет кушать хлеб, крошит его.

3. Пятеро детей (50%) кушают за столом молча;

- четверо детей (40%) иногда разговаривают за столом во время еды;

- один ребенок(10%) постоянно разговаривает.

4. Семеро детей (70%) говорят после еды «спасибо» без напоминания;

- двое детей (20%) не всегда благодарят после еды;

- один (10%) не говорит спасибо.

5. Шестеро детей (60%) умеют пользоваться салфетками после еды;

- четверо детей (40%) не всегда пользуются салфетками после еды.

Отразила навык культуры еды в рисунке 8.

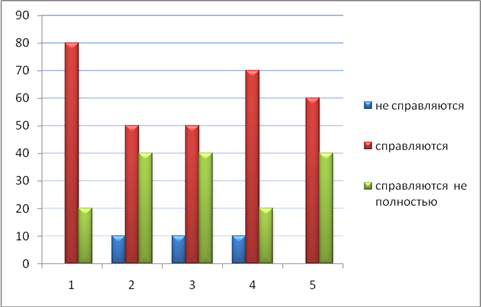
Рисунок 8 - Навык культуры еды

Условные обозначения: 1–держать ложку, 2–не крошить хлеб, 3–не разговаривать за столом, 4–благодарить, 5–пользоваться салфеткой.

Диагностика навыка раздевания и одевания.

1. Умеют расстёгивать пуговицы шестеро детей (60%);

- двое детей делают это с помощью взрослых(20%);

- двое человек(20%) не умеют расстёгивать пуговицы.

2. Снимает самостоятельно платье и брюки пятеро (50%);

Образование, педагогика, воспитание:

Графика. Стили и материалы. Особенности выполнения графических работ
Во-первых, графика это искусство, основой которого является рисунок. Линия, пятно и светотень являются основными изобразительными средствами графики. График, используя контрасты только черного и белого в рисунке или гравюре, убедительно передает широкий слепящий поток открытого прямого света. Цвет ...

Учебник математики
Назначение учебника математики Учебник математики – книга, излагающая основы научных знаний по математике в соответствии с целями обучения, определёнными программой и требованиями дидактики. Содержание и построение учебника определяется задачами преподавателя математики и спецификой предмета и пото ...

Методы, способствующие развитию познавательной активности учащихся на уроках биологии
Степень активности учащихся является реакцией, методы, и приемы работы преподавателя являются показателем его педагогического мастерства. Активными методами обучения следует называть те, которые максимально повышают уровень познавательной активности школьников, побуждают их к старательному учению. ...