Организация работы по взаимодействию с родителями

Январь

Участие родителей в проведении зимних каникул.

Участие в празднике «Лыжня зовет».

Изготовление ширм «Пушкин — малышам» в старшей и подготовительной к школе группах.

Открытые занятия совместно с родителями по ознакомлению с окружающим, развитию речи и математике.

Февраль

Консультации: «Физическое воспитание детей в семье» (1-я младшая группа); «О детях с ослабленным здоровьем» (младшая группа).

Художественно-эстетическое воспитание дошкольников: концерт детей ДОУ; выставка детского творчества; ярмарка. Распродажа работ, сделанных руками детей и родителей.

Участие родителей в празднике «Масленица».

Март

Консультации на темы: «Воспитание у детей внимания и усидчивости» (старшая группа); «Воспитание умственной активности в играх и на занятиях» (подготовительная к школе группа).

Апрель

Месяц открытых занятий.

Консультации врача, психолога, логопеда на тему «Готов ли ваш ребенок к обучению в школе? »

Май

Круглый стол: результаты диагностических методик (участие специалистов ДОУ); наблюдения в природе.

Консультации на темы: «С ребенком на дачном участке»; «Здравствуй, лето!»; «Наблюдения в природе».

Большую роль играет наглядная информация для родителей.

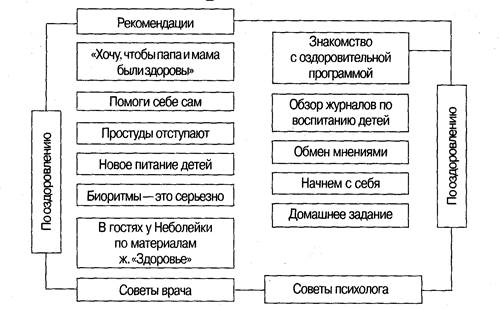
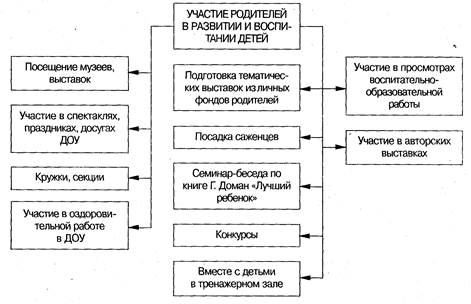
Рис. 2. Разделы наглядной информации для родителей

Образование, педагогика, воспитание:

Задания – элемент методической системы
Задания как элемент методической системы, используемой для развития умения учащихся рассуждать, должна составлять определенную совокупность. Неупорядоченное стихийное применение заданий в обучении полезно, необходимо, но недостаточно для достижения каждым учеником должного уровня развития этого уме ...

Особенности методики организации и проведения игр-драматизаций с детьми старшего дошкольного возраста в условиях дошкольного образовательного учреждения
Наиболее эффективными сюжетами для игр-драматизаций, с точки зрения развития навыков театрализованной игры, являются сюжеты сказок. Особая роль при этом отводится сюжетам русских народных сказок, которые радуют детей своим оптимизмом, добротой, любовью ко всему живому, мудрой ясностью в понимании ж ...

Типология и качества мышления
Формы мышления В психологической науке различают такие логические формы мышления как: понятия; суждения; умозаключения. Понятие - это отражение в сознании человека общих и существенных свойств предмета или явления. Понятие - форма мышления, которая отображает единичное и особенное, являющееся однов ...