Почленное дифференцирование функциональных рядов

Теорема 7. Пусть последовательность функций , непрерывно дифференцируемых на , и последовательность их производных равномерно сходятся на , тогда предел последовательности непрерывно дифференцируемых функций , т.е. , непрерывно дифференцируем на указанном отрезке и верно равенство:

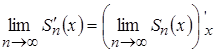или

.

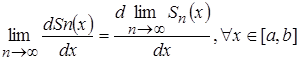Доказательство

Обозначим через предельную функцию последовательностей функций : .

По условию теоремы равномерно сходится к предельной функции на .

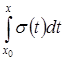На основании ранее доказанных теорем функция непрерывна на , следовательно, она будет интегрируема на, т.е. существует , он будет равен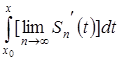 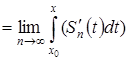(на основании теоремы о почленном интегрировании функциональных последовательностей).

По свойству определенного интеграла: 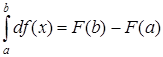, правую часть записанного выражения можно записать в виде следующего равенства: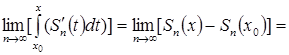 (на основании теоремы о предельной сумме сходящихся последовательностей) и видно, что функция дифференцируема для .

Известна теорема, что если функция дифференцируема в точке, то она непрерывна в этой точке. Значит, функция непрерывна .

В соответствии с теоремой, если функция непрерывна на , то она на нем интегрируема, т.е. существует 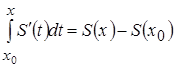. Следовательно, функция непрерывна в каждой точке .

Из пунктов 4),

5), и 6) следует, что функция непрерывно дифференцируема на указанном отрезке.

Теорема доказана [14].

Следствие. Пусть функции непрерывно дифференцируемы на и функциональные ряды: 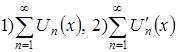равномерно сходятся на . Тогда сумма функционального ряда 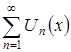непрерывно дифференцируема на указанном отрезке и верно равенство:

=

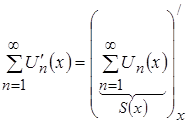(т.е. допустимо почленное дифференцирование у такого функционального ряда).

Доказательство

Обозначим предел частичных сумм , т.е. для функционального ряда 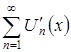. По условию следствия должны равномерно сходиться последовательности функций . На основании только что доказанной теоремы и функция непрерывно дифференцируема, т.е. . Последнее равенство можно переписать по-другому:

Образование, педагогика, воспитание:

Неурочные формы внеклассной работы
Спортивные соревнования являются одной из самых интересных, увлекательных форм внеклассной работы по физическому воспитанию в начальной школе. Они содействуют привлечению учащихся к систематическим занятиям физическими упражнениями дома и в коллективе физкультуры, повышают физическую подготовленнос ...

Методы, способствующие развитию познавательной активности учащихся на уроках биологии
Степень активности учащихся является реакцией, методы, и приемы работы преподавателя являются показателем его педагогического мастерства. Активными методами обучения следует называть те, которые максимально повышают уровень познавательной активности школьников, побуждают их к старательному учению. ...

Применение дидактических игр на уроках математики во 2 классе
Учащихся вторых классов больше всего увлекает в игре её результат. У них проявляется тяга к играм на соревнование. В начале их увлекает желание одержать личную победу, стать победителем в соревновании между учениками в классе. Постепенно интересы ученика расширяются, он переживает не только свой ли ...