Определения равномерно сходящихся функциональных последовательностей и рядов

Опр.5. Последовательность функций равномерно сходится на множестве Х к предельной функции , если

.

Опр.6. Функциональная последовательность называется равномерно сходящейся на множестве X, если существует функция , в которой она равномерно сходится на множестве X. Обозначение:

.

Геометрический смысл равномерной сходимости функциональной последовательности

Перепишем неравенство опр.5 в виде двойного неравенства:

.

Это означает, что график функций целиком располагается в полосе шириной , и функции и получены смещением функции вверх и вниз на величину .

Рис.1.

Понятие равномерной сходимости естественным образом переносится и на функциональные ряды.

§4. Определения равномерной сходимости функциональных рядов

Опр.7. Если последовательность частичных сумм функционального ряда равномерно сходится к функции на множестве X, то ряд равномерно сходится на множестве X [14].

Рассмотрим определение равномерной сходимости функционального

ряда на некотором отрезке .

Пусть функциональный ряд 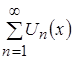сходится на отрезке к функции и - какое-нибудь значение из области сходимости, причем .

Тогда числовой ряд

сходится и его сумма равна , т.е.

=

Представим это равенство в виде

=,

где - n-я частичная сумма; - остаток ряда.

Тогда,

,

.

Как и в случае функциональной последовательности, для функционального ряда номер также зависит как от , так и от значения из области сходимости: . Однако, для функционального ряда число может и не зависеть от , т.е. это число будет одно и тоже для каждого значения , принадлежащего области сходимости.

Опр.8. Функциональный ряд , сходящийся на отрезке , называется равномерно сходящимся, если для любого существует такой номер , не зависящий от , что при , каково бы ни было .

Образование, педагогика, воспитание:

Понятие о технологии конструирования педагогического процесса
Одним из решающих условий успешного протекания педагогического процесса является его конструирование, включающее в себя анализ, диагностику, определение прогноза и разработку проекта деятельности. На этом этапе решения педагогической задачи можно выделить тесно связанные между собой виды деятельнос ...

Цели профессионального образования
Цели профессионального образования выполняют системообразующую функцию в педагогической деятельности. Именно от выбора целей в наибольшей степени зависит выбор содержания, методов и средств обучения и воспитания. Виды педагогических целей многообразны. Можно выделить нормативные государственные цел ...

Цели образования и структурные элементы содержания общего образования
В Концепции модернизации российского образования до 2020 года, исходя из роли образования в развитии российского общества, тенденции мирового развития, определяются, новые социальные требования к системе образования в России. Развивающемуся российскому обществу нужны современно образованные, нравст ...