Определения равномерно сходящихся функциональных последовательностей и рядов

Пример №2. Исследовать на сходимость функциональный ряд

.

Решение

При сумма ряда равна нулю; при ряд, являясь суммой бесконечно убывающей геометрической прогрессии, имеет сумму 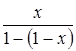. При сумма ряда равна единице. При и ряд представляет собой сумму бесконечно возрастающей геометрической прогрессии, следовательно, расходится.

Таким образом, данный ряд сходится на отрезке и имеет сумму

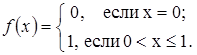
Выясним теперь, будет ли данный ряд равномерно сходящимся на отрезке .

Остаток ряда имеет вид

Очевидно, что . Ряд в правой части равенства представляет собой сумму бесконечно убывающей геометрической прогрессии, поэтому .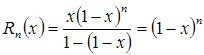

Для того чтобы выполнялось неравенство , нужно положить , откуда или .

Пусть - ближайшее из натуральных чисел, следующих за числом . Тогда для любого положительного числа существует такое натуральное число , зависящее от , что при . Для каждого заданного можно найти соответствующее , определяемое отношением . Однако если , меняясь, приближается к нулю, то также будет приближаться к нулю, а число - неограниченно возрастать. Это обстоятельство показывает, что, хотя данный ряд и сходится на отрезке [0,1], все же для любого положительного числа нельзя найти такой не зависящий от значения номер , что при . Это говорит о том, что ряд не всюду на отрезке [0,1] сходится равномерно. Данный ряд, однако, будет равномерно сходящимся на , где - положительное постоянное число, меньшее 1. В качестве номера (не зависящего от ) можно взять ближайшее из натуральных чисел, следующих за числом [2].

Образование, педагогика, воспитание:

Возможности хоккея в реализации задачи физического воспитания детей старшего дошкольного возраста
В примерной основной общеобразовательной программе дошкольного образования "Детство", которая полностью соответствует Федеральным государственным требованиям, в образовательной области "Физическая культура" предусмотрено обучению игре в баскетбол детей шестого и седьмого года жи ...

Методика подбора и применения средств физического воспитания в период эксперимента
Организация физического воспитания, существующая в настоящее время, направлена в основном на совершенствование двигательных умений и навыков и не в полной мере способствует формированию эмоционально-волевой готовности детей к обучению в школе, поскольку не содержит целевых установок для работы в да ...

Анализ профессионального образа педагога на примере средней общеобразовательной школы
Учитывая, что не каждый педагог целенаправленно задумывается о формировании собственного профессионального имиджа, следует при исследовании акцентировать внимание педагогов на определенные высказывания, касающихся восприятия учащимися некоторых характеристик личности педагога. Суждения, представлен ...