Выявление интереса у детей подготовительной к школе группы к играм с элементами спорта

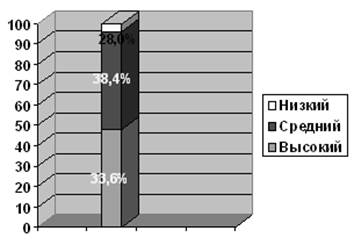
Рис. 1. Уровни развития быстроты у детей подготовительной группы на начало года.

На констатирующем этапе с целью выявления интереса у детей подготовительной группы к подвижным играм, а также знания детьми подвижных игр была проведена индивидуальная беседа с детьми подготовительной группы по следующим вопросам:

Любишь ли ты ходить в детский сад?

Чем ты любишь заниматься в детском саду?

Любишь ли ты играть?

Нравиться ли играть тебе в подвижные игры?

В какие подвижные игры ты любишь играть?

Какие спортивные тгры ты знаешь?

Расскажи, как в них играть?

Ответы детей на первый вопрос показали, что 14 детей, (78,4%), предпочли детский сад дому, четверым детям больше нравится дома (21.2%)/ Все дети любят играть (помимо других занятий). Играть в подвижные игры любят 16 детей (89,6%). Большинство детей любят играть с мячом, обручем, скакалками, любят бегать, среди подвижных игр названы "Гуси-лебеди", (56% детей), 10 детей, "Кто быстрее добежит до флажка" (84 % детей), 16 детей, "Зайцы и волк" (67,2 % детей), 12 детей, "Уголки" (44,8% детей), 8 детей, "Мышеловка" (50,4% детей), "Прятки", "Перелет птиц" (56%). В хоккей любят играть двое детей – 13,2% (cм. табл. 2), (см. диаграмму - рис. 2). Спортивные игры дети знают недостаточно.

Таблица 2

Уровни интереса детей подготовительной группы к спортивным играм на начало года

Образование, педагогика, воспитание:

Психолого-педагогическое обоснование использования наглядного метода обучения
Наглядность – это свойство, выражающее степень доступности и понятности психических образов объектов познания для познающего субъекта. В процессе создания образа восприятия объекта наряду с ощущением участвуют память и мышление. Образ воспринимаемого объекта является наглядным только тогда, когда ч ...

Основные направления логопедической работы по формированию фонематического восприятия у дошкольников с ФФН
Преодоление фонетико-фонематического недоразвития достигается путем целенаправленной логопедической работы по коррекции звуковой стороны речи и фонематического недоразвития. «Система обучения и воспитания детей дошкольного возраста с фонетико-фонематическим недоразвитием включает коррекцию речевого ...

Воспитание самостоятельности и активности
Главной задачей интеллектуальной готовности ребенка является формирование у ребенка определенных знаний и умений на основе включения его в активную учебную деятельность. В процессе решения этой задачи педагог использует разнообразные методы и приемы: объяснение, показ, вопросы, оценка и др. Формиро ...