Определения функциональной последовательности и функционального ряда

Опр.1. Пусть дана последовательность функций: , причем функции являются функциями одной переменной и определены в некоторой области . Такая последовательность называется функциональной и обозначается: .

Пусть для каждого эта последовательность имеет конечный предел. Величина этого предела зависит от значения . Поэтому функциональная последовательность своим пределом будет также иметь функцию, зависящую от , т.е. .

Опр.2. Функция называется предельной функцией последовательности .

Теперь нас будут интересовать не только существование предела при каждом отдельном значении , но и функциональные свойства предельной функции .

Опр.3. Рассмотрим ряд, элементами которого являются функции одной и той же переменной , заданной в области :

.

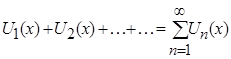Такой ряд называется функциональным рядом.

Сходимость этого ряда определяется следующим образом: при каждом фиксированном значении функция принимает числовое значение. Поэтому при каждом из X функциональный ряд превращается в числовой ряд.

Пусть дан функциональный ряд 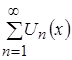и он сходится при каждом фиксированном из, тогда сумма такого ряда представляет собой некоторую функцию от переменной x: 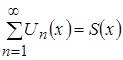. Сумма для функционального ряда определяется также как и для числового: . Здесь - частичная сумма функционального ряда n-го порядка

.

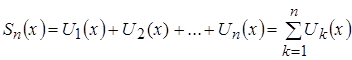Опр.4. Множество всех значений x, при которых заданный функциональный ряд сходится, называется областью сходимости функционального ряда.

Пример №1. Найти область сходимости ряда

.

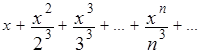Решение. Применим признак Д`Аламбера абсолютной сходимости функционального ряда. Имеем:

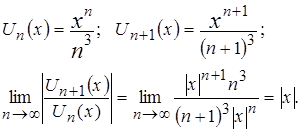
Следовательно, при данный ряд сходится абсолютно, а при расходится.

Рассмотрим теперь поведение исследуемого функционального ряда при и .

При этих значениях получаются соответствующие числовые ряды:

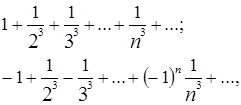
которые, сходятся по интегральному признаку сходимости числового положительного ряда и признаку сходимости знакочередующегося ряда соответственно.

Окончательно получаем, что на отрезке [-1,1] заданный функциональный ряд абсолютно сходится.

Образование, педагогика, воспитание:

Влияние ИЗО искусства на формирование полноценности речи
Развитие речи учащихся на уроках рассматривается нами с позиции неразрывной связи интеллекта, эмоциональной сферы и личности в целом. Коммуникативно-деятельностный подход к развитию речи, осуществляемый на этих уроках, предполагает учет структуры речевой деятельности, развитие различных ее видов. О ...

Теория игры. Виды игры
Ведущие зарубежные и отечественные педагоги рассматривают игру как одно из наиболее эффективных средств организации жизни детей и их совместной деятельности. Игра отражает внутреннюю потребность детей в активной деятельности, это средство познания окружающего мира; в игре дети обогащают свой чувств ...

Трудности овладения учащимися старших классов чтением иноязычных художественных текстов
При обучении иностранному языку чтение рассматривается как самостоятельный вид речевой деятельности и занимает одно из главных мест по своей важности и доступности. Задача учителя при этом заключается не только в том, чтобы научить учащихся читать и понимать тексты на изучаемом языке, но и привить ...